
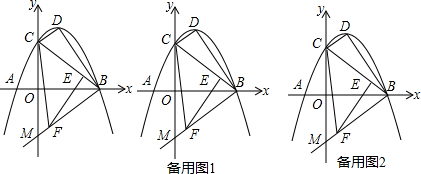
分析 (1)设交点式y=a(x+2)(x-6),再把C点坐标代入求出a=-$\frac{\sqrt{2}}{4}$,则可得到抛物线解析式为y=-$\frac{\sqrt{2}}{4}$x2+$\sqrt{2}$x+3$\sqrt{2}$,然后把解析式配成顶点式即可得到顶点D的坐标;
(2)利用两点间的距离公式计算出CD=$\sqrt{6}$,BD=4$\sqrt{3}$,BC=3$\sqrt{6}$,再利用勾股定理的逆定理判断△BCD是直角三角形,∠BDC=90°,
(3)①利用BM∥CD可得∠DBM=90°,再利用等角的余角相等得到∠DBC=∠EFB,然后根据相似三角形的判定方法得到△EBF∽△DCB;由于△EBF∽△DCB,则利用相似比可计算出EF=2$\sqrt{2}$t,然后分类讨论:当△EFC∽△DCB时,$\frac{EF}{DC}$=$\frac{EC}{DB}$,即 $\frac{2\sqrt{2}t}{\sqrt{6}}$=$\frac{3\sqrt{6}-t}{4\sqrt{3}}$;当△EFC∽△DBC时,$\frac{EF}{DB}$=$\frac{EC}{DC}$,即$\frac{2\sqrt{2}t}{4\sqrt{3}}$=$\frac{3\sqrt{6}-t}{\sqrt{6}}$,再分别利用比例性质求出t即可;
②利用三角形面积公式得到S=S△ECF-S△EBF=$\frac{1}{2}$EF(CE-BE)=-2$\sqrt{2}$t2+6$\sqrt{3}$t,利用二次函数的性质,当t=$\frac{3\sqrt{6}}{4}$时,S取最大值.
解答 (1)解:设抛物线解析式为y=a(x+2)(x-6),
把C(0,3$\sqrt{2}$)代入得a•2•(-6)=3$\sqrt{2}$,
解得a=-$\frac{\sqrt{2}}{4}$,
所以抛物线解析式为y=-$\frac{\sqrt{2}}{4}$(x+2)(x-6),即y=-$\frac{\sqrt{2}}{4}$x2+$\sqrt{2}$x+3$\sqrt{2}$,
∵y=-$\frac{\sqrt{2}}{4}$(x-2)2+4$\sqrt{2}$,
∴顶点D的坐标为(2,4$\sqrt{2}$);
(2)证明:如图1,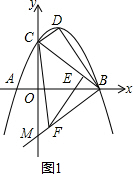
∵B(6,0),C(0,3$\sqrt{2}$),D(2,4$\sqrt{2}$),
∴CD=$\sqrt{{2}^{2}+(4\sqrt{2}-3\sqrt{2})^{2}}$=$\sqrt{6}$,BD=$\sqrt{(2-6)^{2}+(4\sqrt{2})^{2}}$=4$\sqrt{3}$,BC=$\sqrt{{6}^{2}+(3\sqrt{2})^{2}}$=3$\sqrt{6}$,
∵($\sqrt{6}$)2+(4$\sqrt{3}$)2=(3$\sqrt{6}$)2,
∴CD2+BD2=BC2,
∴△BCD是直角三角形,∠BDC=90°;
(3)①证明:如图2,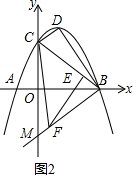
∵BM∥CD,
而∠BDC=90°,
∴∠DBM=90°,
即∠DBC+∠FBC=90°,
∵FE⊥BC,
∴∠FBE+∠EFB=90°,
∴∠DBC=∠EFB,
而∠BDC=∠FEB,
∴△EBF∽△DCB;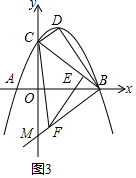
∵△EBF∽△DCB,
∴$\frac{EF}{BD}$=$\frac{BE}{CD}$,即$\frac{EF}{4\sqrt{3}}$=$\frac{t}{\sqrt{6}}$,解得EF=2$\sqrt{2}$t,
当△EFC∽△DCB时,$\frac{EF}{DC}$=$\frac{EC}{DB}$,即 $\frac{2\sqrt{2}t}{\sqrt{6}}$=$\frac{3\sqrt{6}-t}{4\sqrt{3}}$,解得t=$\frac{\sqrt{6}}{3}$.
当△EFC∽△DBC时,$\frac{EF}{DB}$=$\frac{EC}{DC}$,即$\frac{2\sqrt{2}t}{4\sqrt{3}}$=$\frac{3\sqrt{6}-t}{\sqrt{6}}$,解得t=$\frac{3}{2}$$\sqrt{6}$.
综上所述,t的值为$\frac{\sqrt{6}}{3}$或$\frac{3}{2}$$\sqrt{6}$;
②解:S=S△ECF-S△EBF=•CE•EF-BE•EF=EF(CE-BE)=•2$\sqrt{2}$t•(3$\sqrt{6}$-t-t)=-2$\sqrt{2}$t2+6$\sqrt{3}$t,当t=-$\frac{6\sqrt{3}}{2×(-2\sqrt{2})}$=$\frac{3\sqrt{6}}{4}$时,S取最大值.
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质和相似三角形的判定与性质;会用待定系数法求抛物线解析式;能运用勾股定理的逆定理证明直角三角形;理解坐标与图形性质,能利用两点间的距离公式计算线段的长和运用相似比计算线段的长.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
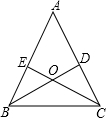 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com