
| ������Χ ��ǧ�ˣ� | 0��50���� ����50�� | 50���ϡ�150���֣���150������50�� | 150���ϡ�250���֣���250������150�� | 250���ϲ��� ������250�� |
| �� ��Ԫ�� | ���ۼ۵�95% | ���ۼ۵�85% | ���ۼ۵�75% | ���ۼ۵�70% |
���� ��1�����ݼס������ҵ��Żݰ취�ֱ�������ҹ�����Ҫ�ķ��þͿ����ˣ�
��2�����ݼס������ҵ��Żݰ취�ֱ�������ҹ�����Ҫ�ķ��ã�Ȼ���ٱȽ����С�Ϳ��ԣ�
��3�����������г�ʽ�ӷֱ��ʾ������xǧ�˸�������Ӧ�ķ��þͿ����ˣ�
��� �⣺��1�������⣬�ã�
�ף�80��6��90%=432��Ԫ����
�ң�50��6��95%+30��6��85%=438��Ԫ����
��
��2�������⣬��
�ף�180��6��85%=918��Ԫ����
�ң�50��6��95%+100��6��85%+30��6��75%=930��Ԫ��
918��930��
���ڼ��������㣻
��3���ף�200��6��85%+��x-200����6��80%=4.8x-60��
�ң�50��6��95%+100��6��85%+��x-200����6��75%=4.5x-105��
���� ������һ��һԪһ�η��̵�Ӧ���⣬�������д���ʽ�������ʽ��ֵ�Լ���ѧʵ�������еķ�����Ƽ�ʵ�����⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ھ���ABCD�У�AB=6��BC=4������P�ӵ�B����������B��C��D��A��ֹͣ�����P�˶���·��Ϊx����ABP�����Ϊy������x��ʾy��
�ھ���ABCD�У�AB=6��BC=4������P�ӵ�B����������B��C��D��A��ֹͣ�����P�˶���·��Ϊx����ABP�����Ϊy������x��ʾy���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����y=x+$\frac{1}{x}$��x��0����ͼ����ͼ��ʾ�����е�x=1ʱ������ȡ����Сֵ2������ͼ����������⣺
��֪����y=x+$\frac{1}{x}$��x��0����ͼ����ͼ��ʾ�����е�x=1ʱ������ȡ����Сֵ2������ͼ����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��0����P�Ǻ���y=x��x��0��ͼ����һ�㣬PQ��AP��y���ڵ�Q�����P�ĺ�����Ϊa����Q��������Ϊb����OP��10$\sqrt{2}$����b��ȡֵ��Χ��
��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��0����P�Ǻ���y=x��x��0��ͼ����һ�㣬PQ��AP��y���ڵ�Q�����P�ĺ�����Ϊa����Q��������Ϊb����OP��10$\sqrt{2}$����b��ȡֵ��Χ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
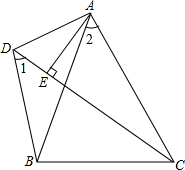 ��ͼ���ڡ�ABC�У�AB=AC����1=��2��AE��CD�ڵ�E��
��ͼ���ڡ�ABC�У�AB=AC����1=��2��AE��CD�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
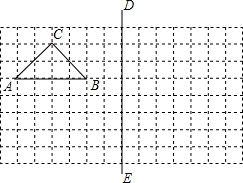 ��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ���������и��⣺
��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ���������и��⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com