
【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y= ![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE. 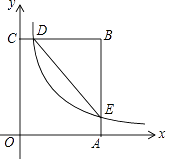
(1)连接OE,若△EOA的面积为3,则k=;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】
(1)6
(2)解:连接DB′,
设D( ![]() ,5),E(3,
,5),E(3, ![]() ),
),
∴BD=3﹣ ![]() ,BE=5﹣
,BE=5﹣ ![]() ,
,
∴tan∠BDE= ![]() =
= ![]() =
= ![]() ,
,
∵B与B′关于DE对称,
∴DE是BB′的中垂线,
∴BB′⊥DE,BG=B′G,DB′=BD,
∴∠DGB=90°,
∴∠BDE+∠DBB′=90°,
∠CB′B+∠DBB′=90°,
∴∠BDE=∠CB′B,
∴tan∠BDE=tan∠CB′B= ![]() =
= ![]() =
= ![]() ,
,
∴CB′= ![]() ,
,
设CD=x,则BD=B′D=3﹣x,
则 ![]() ,
,
∴x= ![]() ,
,
∴D( ![]() ,5).
,5).
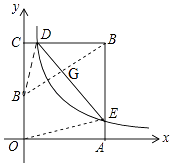
【解析】解:(1)连接OE,如图1,
∵Rt△AOE的面积为3,
∴k=2×3=6.
所以答案是:6;
【考点精析】根据题目的已知条件,利用比例系数k的几何意义的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B. 在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则△ABC为直角三角形
C. 在△ABC中,若a=![]() c,b=
c,b=![]() c,则△ABC为直角三角形
c,则△ABC为直角三角形
D. 在△ABC中,若a∶b∶c=2∶2∶4,则△ABC为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
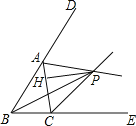
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
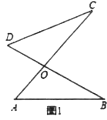
【题目】小学我们已经知道三角形三个内角和是180°,对于如图1中,![]() ,
,![]() 交于
交于![]() 点,形成的两个三角形中的角存在以下关系:①
点,形成的两个三角形中的角存在以下关系:①![]() ;②
;②![]() .试探究下面问题:
.试探究下面问题:
已知![]() 的平分线
的平分线![]() 与
与![]() 的平分线
的平分线![]() 交于点
交于点![]() ,
,
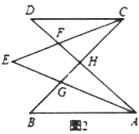
(1)如图2,若![]() ,
,![]() ,
,![]() ,则
,则![]() _________;
_________;
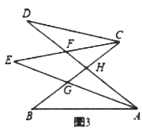
(2)如图3,若![]() 不平行
不平行![]() ,
,![]() ,
,![]() ,则
,则![]() _______.
_______.
(3)在总结前两问的基础上,借助图3,探究![]() 与
与![]() 、
、![]() 之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了支持国货,哈市某手机卖场计划用![]() 万元购进华为品牌手机.从卖场获知华为品牌
万元购进华为品牌手机.从卖场获知华为品牌![]() 种不同型号的手机的进价及售价如下表:
种不同型号的手机的进价及售价如下表:
|
|
| |
进价(元/部) |
|
|
|
售价(元/部) |
|
|
|
若该手机卖场同时购进两种不同型号的手机![]() 台,
台,![]() 万元刚好用完.
万元刚好用完.
(1)请您确定该手机的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售的利润![]() 的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=kx+1(k≠0)与双曲线y= ![]() (x>0)相交于P(1,m).
(x>0)相交于P(1,m). 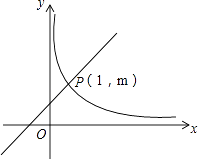
(1)求k的值;
(2)若点Q与点P关于y=x成轴对称,求点Q的坐标为
(3)若过P、Q两点的抛物线与y轴的交点为N(0, ![]() ),求该抛物线的解析式,并求出抛物线的对称轴方程.
),求该抛物线的解析式,并求出抛物线的对称轴方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
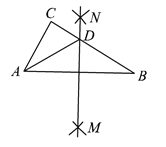
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于![]() AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为16,△ABC的周长28,则AB为___________.
AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为16,△ABC的周长28,则AB为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com