
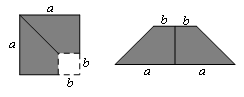
如下图,在边长为![]() 的正方形中,剪去一个边长为
的正方形中,剪去一个边长为![]() 的小正方形(
的小正方形(![]() ),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于
),将余下部分剪开后拼成一个梯形,根据两个图形阴影面积的关系,可以得到一个关于![]() ,
,![]() 的恒等式为( ).
的恒等式为( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
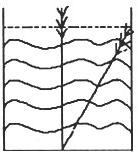 在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如下图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如下图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
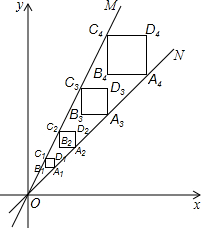 如下图所示,正方形A1B1C1D1、正方形A2B2C2D2,正方形A3B3C3D3、…,正方形AnBnCnDn均位于第一象限内,它们的边平行于x轴或y轴,其中点A1,A2,…,An在直线y=x上,点C1,C2,…,Cn在直线y=2x上.
如下图所示,正方形A1B1C1D1、正方形A2B2C2D2,正方形A3B3C3D3、…,正方形AnBnCnDn均位于第一象限内,它们的边平行于x轴或y轴,其中点A1,A2,…,An在直线y=x上,点C1,C2,…,Cn在直线y=2x上.查看答案和解析>>
科目:初中数学 来源:2007年江苏地区数学中考动态型试题-新人教 题型:059
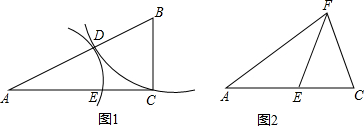
如下图,在边长为2个单位长度的正方形ABCD中,点O、E分别是AD、AB的中点,点F是以点O为圆心、OE的长为半径的圆弧与DC的交点,点P是![]() 上的动点,连结OP,并延长交直线BC于点K.
上的动点,连结OP,并延长交直线BC于点K.
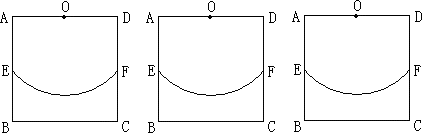
(1)当点P从点E沿![]() 运动到点F时,点K运动了多少个单位长度?
运动到点F时,点K运动了多少个单位长度?
(2)过点P作![]() 所在圆的切线,当该切线不与BC平行时,设它与射线AB、直线BC分别交于点M、G.
所在圆的切线,当该切线不与BC平行时,设它与射线AB、直线BC分别交于点M、G.
①当K与B重合时,BG∶BM的值是多少?
②在点P运动的过程中,是否存在BG∶BM=3的情况?你若认为存在,请求出BK的值;你若认为不存在,试说明其中的理由.
一般地,是否存在BG∶BM=n(n为正整数)的情况?试提出你的猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:有一个水池,截面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如下图所示,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.那么水深多少?芦苇长为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com