
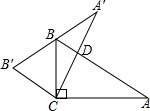
 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角∠A CA′的度数为80°.
如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角∠A CA′的度数为80°. 分析 根据旋转的性质可得∠B′=∠ABC,BC=B′C,根据等腰三角形两底角相等求出∠CBB′=∠B′,根据直角三角形的性质求出∠B=50°,根据三角形内角和定理求出∠BCB′的度数,进而求出旋转角∠A CA′的度数.
解答 解:∵△ABC以点C为中心旋转到△A′B′C的位置,
∴∠B′=∠ABC,BC=B′C′,
∴∠CBB′=∠B′,
∵∠A=40°,
∴∠B′=∠ABC=90°-40°=50°,
∴∠BCB′=180°-2×50°=80°,
∵∠B′CB+∠BCA′=∠ACA′+∠BCA′,
∴∠B′CB=∠ACA′
∴∠ACA′=80°.
故答案为:80°.
点评 本题考查了旋转的性质,等腰三角形的性质,熟记性质并求出BC=B′C是解题的关键,此题难度不大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
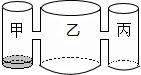 实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm.
实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在容器的5cm高度处连通(即管子底离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升$\frac{5}{6}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,AB=AC,BC=6,BC边上的高AD垂直平分BC,且AD=4,以B为原点,BC所在直线为x轴,建立适当的平面直角坐标系,并求这个三角形三个顶点的坐标.
如图,已知△ABC,AB=AC,BC=6,BC边上的高AD垂直平分BC,且AD=4,以B为原点,BC所在直线为x轴,建立适当的平面直角坐标系,并求这个三角形三个顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.
如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,D、E是以AB为直径的半圆O上任意两点,连接AD、AE、DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加的一个条件是①②③(填正确结论的序号).
如图,D、E是以AB为直径的半圆O上任意两点,连接AD、AE、DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加的一个条件是①②③(填正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点O在AB上,以O为圆心的圆经过A,C两点,交AB于点D,已知∠A=α,∠B=β,且2α+β=90°.若OA=6,sinβ=$\frac{3}{5}$,求BC的长.
如图,在△ABC中,点O在AB上,以O为圆心的圆经过A,C两点,交AB于点D,已知∠A=α,∠B=β,且2α+β=90°.若OA=6,sinβ=$\frac{3}{5}$,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.
在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com