
【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于点F.若BP=4,则PF的长( )
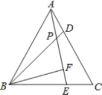
A. 2 B. 3 C. 1 D. 8
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
如图①,若点B把线段分成两条长度相等的线段AB和BC,则点B叫做线段AC的中点.
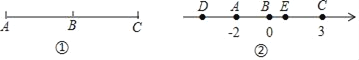
回答问题:
(1)如图②,在数轴上,点A所表示的数是﹣2,点B所表示的数是0,点C所表示的数是3.
①若A是线段DB的中点,则点D表示的数是 ;
②若E是线段AC的中点,求点E表示的数.
(2)在数轴上,若点M表示的数是m,点N所表示的数是n,点P是线段MN的中点.
①若点P表示的数是1,则m、n可能的值是 (填写符合要求的序号);
(i)m=0,n=2;(ii)m=﹣5,n=7;(iii)m=0.5,n=1.5;(iv)m=﹣1,n=2
②直接用含m、n的代数式表示点P表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( ).
![]()
A. 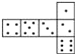 B.
B. 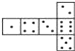 C.
C.  D.
D. 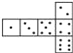
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦. 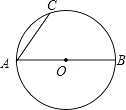
(1)请你按下面步骤画图(画图或作辅助线时先使用铅笔画出,确定后必须使用黑色字迹的签字笔描黑); 第一步,过点A作∠BAC的角平分线,交⊙O于点D;
第二步,过点D作AC的垂线,交AC的延长线于点E.
第三步,连接BD.
(2)求证:AD2=AEAB;
(3)连接EO,交AD于点F,若5AC=3AB,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列多项式的乘法中,不能用平方差公式计算的是( )
A. (a+b)(a-b) B. (x-2y)(-x+2y) C. (x-2y)(-x-2y) D. (![]() x-y)(y+0.5x)
x-y)(y+0.5x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀将其均匀分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中阴影部分的正方形的边长等于________;
(2)请你用两种不同的方法表示图②中阴影部分的面积,方法一:__________________,方法二:________________;
(3)观察图②,你能写出代数式(m+n)2,(m-n)2,mn之间的关系吗?
(4)应用:已知m+n=11,mn=28(m>n),求m,n的值.
 ①
①  ②
②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:2,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
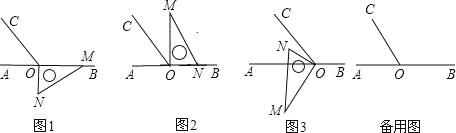
(1)将图1中的三角板绕点O按逆时针方向旋转至图2的位置,使得ON落在射线OB上,此时三角板旋转的角度为 度;
(2)继续将图2中的三角板绕点O按逆时针方向旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角三角板从图1逆时针旋转到图3的位置的过程中,若三角板绕点O按15°每秒的速度旋转,当直角三角板的直角边ON所在直线恰好平分∠AOC时,求此时三角板绕点O的运动时间t的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com