
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
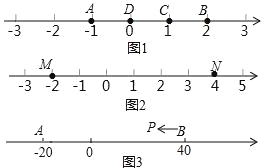
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
【答案】(1)点D是(B,C)的奇异点,不是(A,B)的奇异点;(2)(M,N)的奇异点表示的数是2;(3)①点P表示的数是0或10或20时,P、A、B中恰有一个点为其余两点的奇异点;②PB=120或180或90.
【解析】
(1)根据奇异点的定义和数轴上两点间的距离,即可求出点D到点A的距离为1,到点B的距离为2,以及点D到点C的距离为1,就可以对点D做出判断.
(2)设奇异点表示的数为x,根据奇异点的定义可得方程:x﹣(﹣2)=2(4﹣x).从而求得x值.
(3)①当P在A、B两点之间时,P、A、B中恰有一个点为其余两点的奇异点需分类讨论,具体分四种情况讨论:当点P是(A,B)的奇异点时、当点P是(B,A)的奇异点时、当点A是(B,P)的奇异点时、当点B是(A,P)的奇异点时,计算方法同(1).
②点P到达点A后继续向左运动,是否存在使得P、A、B中恰有一个点为其余两点的奇异点的情况方法同①分四种情况讨论:当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.
(1)在图1中,点D到点A的距离为1,到点B的距离为2,
∴点D是(B,C)的奇异点,不是(A,B)的奇异点;
(2)设奇异点表示的数为x,
则由题意,得x﹣(﹣2)=2(4﹣x).
解得x=2.
∴(M,N)的奇异点表示的数是2;
(3)①设点P表示的数为y.
当点P是(A,B)的奇异点时,
则有y+20=2(40﹣y),
解得y=20.
当点P是(B,A)的奇异点时,
则有40﹣y=2(y+20),
解得y=0.
当点A是(B,P)的奇异点时,
则有40+20=2(y+20),
解得y=10.
当点B是(A,P)的奇异点时,
则有40+20=2(40﹣y),解得y=10.
∴当点P表示的数是0或10或20时,
P、A、B中恰有一个点为其余两点的奇异点.
②当点P为(B,A)的奇异点时,PB=120;
当点A为(P,B)的奇异点时,PB=180;
当点A为(B,P)的奇异点时,PB=90;
当点B为(P,A)的奇异点时,PB=120.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】暑期临近,重庆市某中学校为了丰富学生的暑期文化生活,同时帮助孩子融洽亲子关系,增进亲子间的情感交流,计划组织学生去某景区参加为期一周的“亲子一家游”活动. 若报名参加此次活动的学生人数共有56人,其中要求参加的每名学生都至少需要一名家长陪同参加.
(1)假设参加此次活动的家长人数是参加学生人数的2倍少2人,为了此次活动学校专门为每名学生和家长购买一件T恤衫, 家长的T恤衫每购买8件赠送1件学生T恤衫(不足8件不赠送),学生T恤衫每件15元,学校购买服装的费用不超过3401元,请问每件家长T恤衫的价格最高是多少元?
(2)已知该景区的成人票价每张100元,学生票价每张50元,为了支持此次活动,该景区特地推出如下优惠活动:每张成人票价格下调a%,学生票价格下调.![]() a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了
a% 另外,经统计此次参加活动的家长人数比学生人数多a%, 参加此次活动的购买票价总费用比未优惠前减少了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为D. 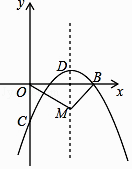
(1)求抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿抛物线的对称轴向下运动,连OM,BM,设运动时间为t秒(t=0),在点M的运动过程中,当∠OMB=90°时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1的正方形,已知学校的坐标为A(2,2).
(1)请在图中建立适当的直角坐标系,并写出图书馆的坐标;
(2)若体育馆的坐标为C(-2,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,cot∠ADB= ![]() ,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
,AB=16.点E在射线BC上,点F在线段BD上,且∠DEF=∠ADB.
(1)求线段BD的长;
(2)设BE=x,△DEF的面积为y,求y关于x的函数关系式,并写出函数定义域;
(3)当△DEF为等腰三角形时,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,∠CFE的大小是( )

A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C 为数轴上三点,若点 C 到点 A 的距离是点 C 到点 B 的距离的 2倍,则称点 C 是(A,B)的奇异点,例如图 1 中,点 A 表示的数为﹣1,点B 表示的数为 2,表示 1 的点 C 到点 A 的距离为 2,到点 B 的距离为 1,则点C 是(A,B)的奇异点,但不是(B,A)的奇异点.
(1)在图 1 中,直接说出点 D 是(A,B)还是(B,C)的奇异点;
(2)如图 2,若数轴上 M、N 两点表示的数分别为﹣2 和 4,(M,N)的奇异点 K 在 M、N 两点之间,请求出 K 点表示的数;
(3)如图 3,A、B 在数轴上表示的数分别为﹣20 和 40,现有一点 P 从点 B 出发,向左运动.
①若点 P 到达点 A 停止,则当点 P 表示的数为多少时,P、A、B 中恰有一个点为其余两点的奇异点?
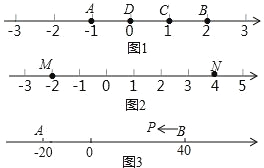
②若点 P 到达点 A 后继续向左运动,是否存在使得 P、A、B 中恰有一个点为其余两点的奇异点的情况?若存在,请直接写出此时 PB 的距离;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com