
【题目】阅读材料,并完成相应任务.
2000多年来,人们对勾股定理的证明颇感兴趣,不但因为这个定理重要、基本,还因为这个定理贴近人们的生活实际,所以很多人都探讨、研究它的证明,新的证法不断出现.
下面的图形是传说中毕达哥拉斯的证明图形:
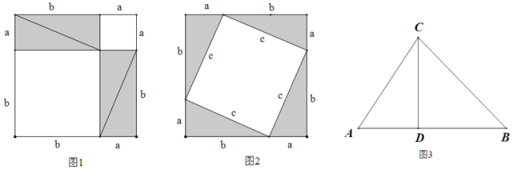
证明:①在图1中,∵![]()
![]() 4个直角三角形的面积+两个正方形的面积
4个直角三角形的面积+两个正方形的面积
=4× + + .
②在图2中,∵![]()
![]() 4个直角三角形的面积+正方形的面积
4个直角三角形的面积+正方形的面积
=4× + .
∴4× + + =4× + .
整理得:![]()
∴ .
任务:(1)将材料中的空缺部分补充完整;
(2)如图3,在△ABC中,∠A=60°,∠ACB=75°,CD⊥AB,AC=4,求BC的长.
科目:初中数学 来源: 题型:
【题目】按要求完成作图:

(1)作出△ABC关于x轴对称的图形;
(2)写出A、B、C的对应点A′、B′、C′的坐标;
(3)在x轴上画出点Q,使△QAC的周长最小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在等腰直角三角形![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .则
.则![]() 、
、![]() 和
和![]() 之间的数量关系是: .
之间的数量关系是: .
(2)如图(2),将(1)中的条件改为:在等腰三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,且
上,且![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论![]() 是否成立?如成立,请你给出证明;若不成立,请说明理由.
是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),![]() 、
、![]() 是直线
是直线![]() 上的两动点(
上的两动点(![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
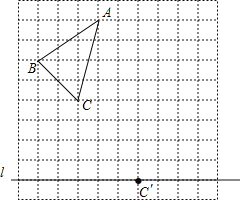
【题目】如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.
(1)画出△A'B'C'.
(2)若连接AA′、BB′,则这两条线段之间的关系是 .
(3)试在直线l上画出格点P,使得由点A'、B'、C'、P四点围成的四边形的面积为9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探究
在综合实践课上,老师让同学们以两个全等的三角形纸片为操作对象,进行相关问题的探究.如图1,△ABC≌△DEF,其中∠ACB=90°,∠A=30°,AB=4.

(1)请直接写出EF= ;
(2)新星小组将这两张纸片按如图2所示的方式放置后,经过观察发现四边形ACBF是矩形,请你证明这个结论.
(3)新星小组在图2的基础上,将△DEF纸片沿AB方向平移至如图3的位置,其中点E与AB的中点重合,连接CE,BF.请你判断四边形BCEF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用手指玩游戏,规则如下:i)每次游戏时,两人同时随机地各伸出一根手指;ii)两人伸出的手指中,大拇指只胜食指,食指只胜中指,中指只胜无名指,无名指只胜小拇指,小拇指只胜大拇指,否则不分胜负,依据上述规则,当甲、乙两人同时随机地各伸出一根手指时,
(1)求甲伸出小拇指取胜的概率;
(2)求乙取胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏的爸爸买了一张嘉峪关的门票,她和哥哥都想去,可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2,3,5,9的四张牌给小敏,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽取一张,然后将抽出的两张牌数字相加,如果和为偶数,则小敏去,如果和为奇数,则哥哥去.
(1)请你用列表或树状图的方法求小敏去的概率.
(2)哥哥设计的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点
于点![]()
(1)如图1,若![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,点![]() 分别在线段
分别在线段![]() 上,将
上,将![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,折痕分别为
处,折痕分别为![]() 和
和![]() ,且点
,且点![]() ,点
,点![]() 均在直线
均在直线![]() 上,若
上,若![]() ,试猜想
,试猜想![]() 与
与![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)在(2)小题的条件下,将![]() 绕点
绕点![]() 逆时针旋转一个角度
逆时针旋转一个角度![]() (
(![]() ),记旋转中的
),记旋转中的![]() 为
为![]() (如图3),在旋转过程中,直线
(如图3),在旋转过程中,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,是否存在这样的
,是否存在这样的![]() 两点,使
两点,使![]() 为直角三角形?若存在,请直接写出旋转角
为直角三角形?若存在,请直接写出旋转角![]() 的度数;若不存在,请说明理由.
的度数;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com