
����Ŀ�������仯������������ĸ߶ȹ�ע���йز�����ȫ����Χ�ڶ�12��35��������Ⱥ��������������飬�õ�������������������ͳ��ͼ�������ͼ����Ϣ����������⣺
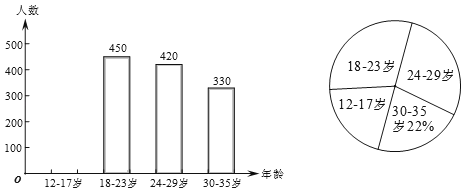
��1���ε����˶����������Ա��
��2��ͨ�����㲹ȫ����ͳ��ͼ��������ͳ��ͼ�У�18��23�겿�ֵ�Բ�ĽǵĶ���Ϊ�� ����
��3��Ŀǰ�ҹ�12��35���������ԼΪ3000�����������12��23���������
���𰸡���1�����ε�����1500�������Ա����2��108������3��12��23���Լ��1500����
��������
��1������30��35�����������ռ�İٷֱȿ�����ñ��ε����˶����������Ա��
��2�����ݣ�1���еĽ���������12��17���������18��23�겿�ֵ��ĽǵĶ�����
��3������ͳ��ͼ�е����ݿ������12��23���������
�⣺��1��330��22%��1500��������
�𣺱��ε�����1500�������Ա��
��2��12��17����У�1500��450��420��330��300���ˣ���
��ȫ������ͳ��ͼ����ͼ��ʾ��
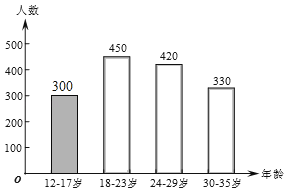
����ͳ��ͼ�У�18��23�겿�ֵ��ĽǵĶ���Ϊ��![]() ��
��
�ʴ�Ϊ��108����
��3��![]() �����ˣ���
�����ˣ���
��12��23���Լ��1500���ˣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��������
��������![]() ��������
��������![]() ��
��![]() �����һ������Ϊ��
�����һ������Ϊ��![]() ����
����![]() ����������һ�㣬����
����������һ�㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() .
.
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ����
����![]() �ڵ������ޣ���
�ڵ������ޣ���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() �����ֵ����ʱ��
�����ֵ����ʱ��![]() �����ꣻ
�����ꣻ
![]() ����
����![]() ����
����![]() ,��ֱ��д����ʱ��
,��ֱ��д����ʱ��![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BC��9����ABC��ƽ����BF��AC�ڵ�F����D����E�ֱ��DZ�AB��AC�ϵĵ㣬��![]() ����BD��DE��ֵΪ��������
����BD��DE��ֵΪ��������
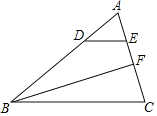
A.3B.3��5C.4D.4��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
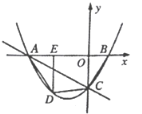
����Ŀ����ͼ��1�������κ���y��ax2��bx��a��0����ͼ����x�ᡢֱ��y��x�Ľ���ֱ�Ϊ��A(4��0)��B(5��5)��

��1��a���� ����b���� ������AOB���� ������
��2������AB����P����������һ�㣨���ڵ�A�����ҡ�PBO����OBA�����P�������� ����
��3����ͼ��2������C��D���߶�OB�ϵĶ��㣬��CD��2![]() �����C�ĺ�����Ϊm��
�����C�ĺ�����Ϊm��
�ٹ���C��D�ֱ���x��Ĵ��ߣ����������ཻ�ڵ�F��E������EF����CF+DEȡ�����ֵʱ����m��ֵ���ж��ı���CDEF����״��
������AC��AD����mΪ��ֵʱ��AC+ADȡ����Сֵ������������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2������AOB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B��C��D������ֱ��ǣ�1��7������1��1������4��1������6��1������C��D��EΪ���������������ABC���ƣ����E�����겻������

A����6��0�� B����6��3�� C����6��5�� D����4��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л������Ͼ�����˾����һ�ֻ���ԭ������ǧ�ˣ��۸�Ϊÿǧ��30Ԫ����۲��Ź涨�����۵��۲�����ÿǧ��60Ԫ��������ÿǧ��30Ԫ�����г����鷢�֣���������y��ǧ�ˣ������۵���x��Ԫ����һ�κ������ҵ�x��45ʱ��y��10��x��55ʱ��y��90�������۹����У�ÿ�컹Ҫ֧����������500Ԫ��
��1�����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����ù�˾���۸�ԭ���ջ���w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��3�������۵���Ϊ����Ԫʱ���ù�˾�ջ�������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵꾭Ӫ�Ҿ����ɺУ���֪��������ʱ�ĵ�����20Ԫ�����鷢�֣����۵�����30Ԫʱ������������230���������۵���ÿ����1Ԫ�����������ͼ���10������ÿ�����ɺ��ۼ۲��ܸ���40Ԫ����ÿ�����ɺе����۵���������![]() Ԫʱ��
Ԫʱ��![]() Ϊ��������������������Ϊ
Ϊ��������������������Ϊ![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2��ÿ�����ɺе��ۼ۶�Ϊ����Ԫʱ������������ǡΪ2520Ԫ��
��3��ÿ����ߵ��ۼ۶�Ϊ����Ԫʱ��ʹ������������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���![]() ����������ȵ�ʵ������
����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2����![]() ��
��![]() ��һԪ���η���
��һԪ���η���![]() ������������
������������![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com