
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与
与![]() 相交于点
相交于点![]() ,下列结论正确的有( )个
,下列结论正确的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等腰三角形;⑤
是等腰三角形;⑤![]() .
.

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
只要证明△BDF≌△CDA,△BAC是等腰三角形,∠DGF=∠DFG=67.5°,即可判断①②③④正确,作GM⊥BD于M,只要证明GH<DG即可判断⑤错误.
∵CD⊥AB,BE⊥AC,
∴∠BDC=∠ADC=∠AEB=90°,
∴∠A+∠ABE=90°,∠ABE+∠DFB=90°,
∴∠A=∠DFB,
∵∠ABC=45°,∠BDC=90°,
∴∠DCB=90°45°=45°=∠DBC,
∴BD=DC,
在△BDF和△CDA中
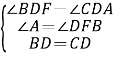 ,
,
∴△BDF≌△CDA(AAS),
∴BF=AC,故①正确.
∵∠ABE=∠EBC=22.5°,BE⊥AC,
∴∠A=∠BCA=67.5°,故③正确,
∴BA=BC,
∵BE⊥AC,
∴AE=EC=![]() AC=
AC=![]() BF,故②正确,
BF,故②正确,
∵BE平分∠ABC,∠ABC=45°,
∴∠ABE=∠CBE=22.5°,
∵∠BDF=∠BHG=90°,
∴∠BGH=∠BFD=67.5°,
∴∠DGF=∠DFG=67.5°,
∴DG=DF,故④正确.
作GM⊥AB于M.
∵∠GBM=∠GBH,GH⊥BC,
∴GH=GM<DG,
∴S△DGB>S△GHB,
∵S△ABE=S△BCE,
∴S四边形ADGE<S四边形GHCE.故⑤错误,
∴①②③④正确,
故选:B.



科目:初中数学 来源: 题型:
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4个小长方形,然后按图2的形状拼成一个正方形.

(1)图2中阴影部分的面积请用两种方法表示:① ;②_________.
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,求x-y的值.
(4)观察图3,你能得到怎样的代数恒等式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
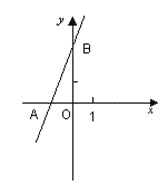
(1)求A,B两点的坐标;
(2)过B点作直线BP与x轴相交于P,且使OP=2OA, 求ΔABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至![]() ,旋转角为
,旋转角为![]() .
.

(1)当点![]() 恰好落在EF边上时,求旋转角
恰好落在EF边上时,求旋转角![]() 的值;
的值;
(2)如图2,G为BC的中点,且00<![]() <900,求证:
<900,求证:![]() ;
;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,![]() 与
与![]() 能否全等?若能,直接写出旋转角
能否全等?若能,直接写出旋转角![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究
小聪将命题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B分为“直角、钝角、锐角”三种情况进行探究.
第一种情况:当∠B 是直角时,如图1,△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL”定理,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B 是锐角时,如图2,BC=EF,∠B=∠E<90°,在射线EM上有点D,使DF=AC,画出符合条件的点D,则△ABC和△DEF的关系是 ;
A.全等 B.不全等 C.不一定全等
第三种情况:当∠B是钝角时,如图3,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E>90°.过点C作AB边的垂线交AB延长线于点M;同理过点F作DE边的垂线交DE延长线于N,根据“ASA”,可以知道△CBM≌△FEN,请补全图形,进而证出△ABC≌△DEF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com