练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】面试时，某人的基础知识、表达能力、工作态度的得分分别是80分、70分、90分，若依次按照30%、30%、40%的比例确定面试成绩，则这个人的面试成绩是_____分．

    【答案】81

    【解析】

    根据加权平均数定义可得．

    解：这个人的面试成绩是80×30%+70×30%+90×40%＝81（分）．

    故答案为：81．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】点M（2，﹣3）到x轴的距离是（ ）
    A.2
    B.﹣3
    C.3
    D.以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个正数x的两个不同的平方根是3a﹣4和1﹣6a，求a及x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

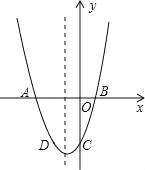
    【题目】已知：二次函数y=x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．

    （1）求抛物线的解析式；

    （2）抛物线的对称轴上有一动点P，求出PA+PD的最小值；

    （3）若抛物线上有一动点P，使三角形ABP的面积为6，求P点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

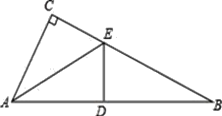
    【题目】已知：如图，在△ABC中，∠C=90°，AE是△ABC的角平分线；ED平分∠AEB，交AB于点D；∠CAE=∠B．

    （1）如果AC=3cm，求AB的长度；

    （2）猜想：ED与AB的位置关系，并证明你的猜想。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

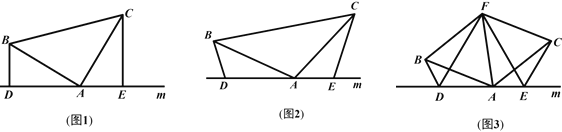
    【题目】（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE＝BD+CE．

    （2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？若成立，请给出证明；若不成立，请说明理由．

    （3）拓展与应用：如图3，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点

    互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一副扑克牌中，拿出红桃2，红桃3，红桃4，红桃5四张牌，洗匀后，小明从中随机摸出一张，记下牌面上的数字为x，然后放回并洗匀，再由小华随机摸出一张，记下牌面上的数字为y，组成一对数（x，y）．则小明、小华各摸一次扑克牌所确定的一对数是方程x+y=5的解的概率为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知m1=3y+1，m2=5y+3，当y=时，m1=m2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（　　）

    A. 方差越大，数据波动越小

    B. 了解辽宁省初中生身高情况适合采用全面调查

    C. 抛掷一枚硬币，正面向上是必然事件

    D. 用长为3cm，5cm，9cm的三条线段围成一个三角形是不可能事件

    查看答案和解析>>

    同步练习册答案