
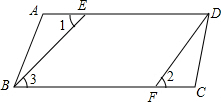
 如图,已知AD∥BC,∠1=∠2,说明BE∥DF的理由.
如图,已知AD∥BC,∠1=∠2,说明BE∥DF的理由.  千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.
如图,⊙O为△ABC的外接圆,AB=AC,AD∥BC交OC的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
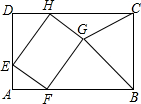 如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.
如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com