
 如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连结CF.
如图,在△ABC中,D,E分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连结CF.分析 (1)由中位线定理,说明EF、BC平行,由边间关系2DE=BC、BE=2DE,说明EF、BC相等,先证明四边形BCFE是平行四边形,再证明四边形BCFE是菱形;
(2)由四边形BCFE是菱形,∠BCF=120°,说明∠ACB=60°,由AE=EC=BC=BE,得到∠A=30°,求出∠ABC的度数,在RT△ABC中,求出AB的长.
解答 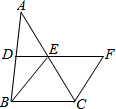 (1)证明:∵D,E分别是AB,AC的中点,
(1)证明:∵D,E分别是AB,AC的中点,
∴DE∥BC,2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC=BE,
∴四边形BCFE是菱形.
(2)解:∵四边形BCFE是菱形,∠BCF=120°,
∴∠ACB=60°,
∵BC=BE,
∴△BEC是等边三角形,
∴∠BEC=60°,
∵E是AC的中点,CE=4,
∴AE=EC=BE=4,∴∠A=30°,
∴∠ABC=180°-∠ACB-∠A=90°.
在Rt△ABC中,AB=$\sqrt{A{C}^{2}-B{C}^{2}}=\sqrt{{8}^{2}-{4}^{2}}=4\sqrt{3}$.
点评 本题考查了三角形的中位线定理、菱形的性质和判定及勾股定理.通过中位线定理把EF与BC连接起来是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在给定的?ABCD中,动点P从BC延长线的某处出发沿射线BC方向运动,PD交BA延长线于点E,在整个运动过程中.△ABP的面积与△ECP的面积的差的值的变化情况是( )
如图,在给定的?ABCD中,动点P从BC延长线的某处出发沿射线BC方向运动,PD交BA延长线于点E,在整个运动过程中.△ABP的面积与△ECP的面积的差的值的变化情况是( )| A. | 不变 | B. | 一直增大 | C. | 先增大后减小 | D. | 先减小后增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,函数y=ax与y=kx+b的图象交于点A(2,3),则关于x的不等式ax<bx+b的解集为( )
如图,函数y=ax与y=kx+b的图象交于点A(2,3),则关于x的不等式ax<bx+b的解集为( )| A. | x>2 | B. | x<2 | C. | x>3 | D. | x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,螺旋形是由一系列等腰直角三角形组成的,其序号依次为①②③④⑤…,若第1个等腰直角三角形的直角边为1,则第2016个等腰直角三角形的面积为22014.
如图,螺旋形是由一系列等腰直角三角形组成的,其序号依次为①②③④⑤…,若第1个等腰直角三角形的直角边为1,则第2016个等腰直角三角形的面积为22014.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com