
【题目】已知二次函数![]() 的部分图象如图,顶点是
的部分图象如图,顶点是![]() .
.
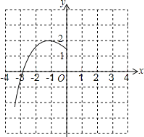
(1)求二次函数的解析式;
(2)若抛物线上两点![]() 、
、![]() 的横坐标满足
的横坐标满足![]() ,则
,则![]() ________
________![]() ;(用“
;(用“![]() ”、“
”、“![]() ”或“
”或“![]() ”填空)
”填空)
(3)观察图象,直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
【答案】(1)y=![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设二次函数顶点式解析式为y=a(x+1)2+2,然后把点(﹣3,0)代入求出a的值,即可得解;
(2)根据x<﹣1时,y随x的增大而减小解答;
(3)根据二次函数的对称性求出抛物线与x轴的另一交点,然后写出x轴上方部分的x的取值范围即可.
(1)∵顶点是(﹣1,2),∴设二次函数顶点式解析式为y=a(x+1)2+2,由图可知,函数图象经过点(﹣3,0),∴a(﹣3+1)2+2=0,解得:a=﹣![]() ,∴二次函数的解析式为y=﹣
,∴二次函数的解析式为y=﹣![]() (x+1)2+2,即y=
(x+1)2+2,即y=![]() ;
;
(2)∵a=﹣![]() <0,二次函数图象对称轴为直线x=﹣1,∴x>﹣1时,y随x的增大而减小,∴﹣1<x1<x2时,y1>y2.
<0,二次函数图象对称轴为直线x=﹣1,∴x>﹣1时,y随x的增大而减小,∴﹣1<x1<x2时,y1>y2.
故答案为:>;
(3)∵函数图象经过(﹣3,0),对称轴为直线x=﹣1,∴二次函数与x轴的另一交点坐标为(1,0),∴y>0时,x的取值范围﹣3<x<1.


科目:初中数学 来源: 题型:
【题目】如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用![]() 长的建筑材料围成,且仓库的面积为
长的建筑材料围成,且仓库的面积为![]() .
.
![]() 求这矩形仓库的长;
求这矩形仓库的长;
![]() 有规格为
有规格为![]() 和
和![]() (单位:
(单位:![]() )的地板砖单价分别为
)的地板砖单价分别为![]() 元/块和
元/块和![]() 元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与
与![]() 相交于点
相交于点![]() ,下列结论正确的有( )个
,下列结论正确的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等腰三角形;⑤
是等腰三角形;⑤![]() .
.

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过点
的图象经过点![]() ,且与二次函数
,且与二次函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点.
两点.
(1)求这两个函数的表达式及![]() 点的坐标;
点的坐标;
(2)在同一坐标系中画出这两个函数的图象,并根据图象回答:当![]() 取何值时,一次函数的函数值小于二次函数的函数值;
取何值时,一次函数的函数值小于二次函数的函数值;
(3)求△BOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程
解:设x2﹣4x=y,
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2﹣4x+4)2(第四步)
(1)该同学第二步到第三步运用了因式分解的 (填序号).
A.提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学在第四步将y用所设中的x的代数式代换,得到因式分解的最后结果.这个结果是否分解到最后? .(填“是”或“否”)如果否,直接写出最后的结果 .
(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以每小时60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止甲、乙两车相距的路程
地,两车分别到达目的地后停止甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示:
(时)之间的函数关系如图所示:
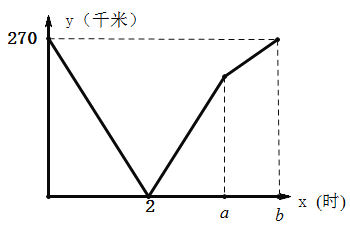
(1)乙年的速度为______千米/时,![]() _____,
_____,![]() ______.
______.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com