
【题目】已知:△ABC 内接于⊙O,过点 A 作⊙O 的切线交 CB 的延长线于点 P,且∠PAB=45°.
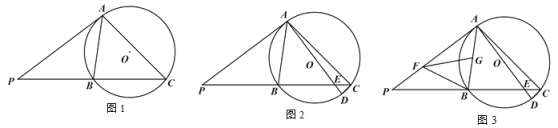
(1)如图 1,求∠ACB 的度数;
(2)如图 2,AD 是⊙O 的直径,AD 交 BC 于点 E,连接 CD,求证:AC CD ![]() ;
;
(3)如图 3 ,在(2)的条件下,当 BC 4![]() CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
CD 时,点 F,G 分别在 AP,AB 上,连接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的长.
【答案】(1)∠ACB=45°;(2)见解析;(3)![]()
【解析】
(1)连接OA,OB,根据切线的性质求出∠OAB=∠OBA=45°,得到∠AOB=90°,再根据圆周角定理可得答案;
(2)作AM⊥BC于M,DN⊥BC于N,连接BD,易求![]() ,
,![]() ,然后证明△ABM≌△BDN,得到AM=BN,等量代换即可得证;
,然后证明△ABM≌△BDN,得到AM=BN,等量代换即可得证;
(3)根据(2)中结论求出![]() ,然后证明△AMC∽△DNC,AM∥DN,根据相似三角形的性质和平行线分线段成比例定理求得DE和AD,进而利用勾股定理求出CD,AC,然后即可求出AB的长,再证明△PAB∽△PCA,求出PA,可得
,然后证明△AMC∽△DNC,AM∥DN,根据相似三角形的性质和平行线分线段成比例定理求得DE和AD,进而利用勾股定理求出CD,AC,然后即可求出AB的长,再证明△PAB∽△PCA,求出PA,可得![]() ,过点G作GK⊥FB,过点F作FH⊥BG,设GK=3b,利用三角函数及等腰三角形的性质求出AH和BH,然后列方程求出b值即可解决问题.
,过点G作GK⊥FB,过点F作FH⊥BG,设GK=3b,利用三角函数及等腰三角形的性质求出AH和BH,然后列方程求出b值即可解决问题.
解:(1)连接OA,OB,则OA=OB,
∴∠OAB=∠OBA,
∵PA是⊙O的切线,
∴∠PAO=90°,
∵∠PAB=45°,
∴∠OAB=∠OBA=45°,
∴∠AOB=90°,
∴∠ACB=![]() ∠AOB=45°;
∠AOB=45°;
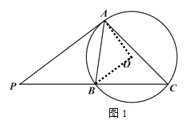
(2)作AM⊥BC于M,DN⊥BC于N,连接BD,
∵AD是⊙O的直径,
∴∠ABD=∠ACD=90°,
∵∠ACB=45°,
∴∠CAM=∠BCD=∠CDN=45°,
∴![]() ,
,![]() ,
,
∵∠ADB=∠ACB=45°,
∴AB=BD,
∵∠ABM+∠DBN=90°=∠BDN+∠DBN,
∴∠ABM=∠BDN,
又∵∠AMB=∠BND=90°,
∴△ABM≌△BDN(AAS),
∴AM=BN,
∴![]() ;
;

(3)如图3,作AM⊥BC于M,DN⊥BC于N,由(2)可知:![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
设CD=x,则AC=7x,
∵∠AMC=∠DNC=90°,∠ACM=∠DCN=45°,
∴△AMC∽△DNC,
∴![]() ,
,
∵AM⊥BC,DN⊥BC,
∴AM∥DN,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在Rt△ACD中,AC2+CD2=AD2,
∴![]() ,
,
解得:![]() (负值已舍去),
(负值已舍去),
∴![]() ,
,![]() ,
,![]() ,
,
∵△AMC是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴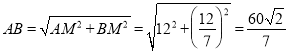 ,
,
∵∠P=∠P,∠PAB=∠PCA=45°,
∴△PAB∽△PCA,
∴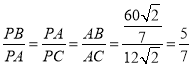 ,
,
设PB=5a,则PA=7a,
由PA2=PB·PC得:![]() ,
,
解得:![]() 或a=0(舍去),
或a=0(舍去),
∴PA=20,
∴![]() ,
,
∴![]() ,
,
过点G作GK⊥FB,过点F作FH⊥BG,
设GK=3b,则BF=FG=5b,
∴FK=4b,
∴BK=b,
∴![]() ,
,
∴BH![]() ,
,
∴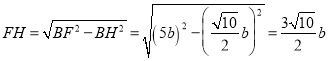 ,
,
∵∠PAB=45°,
∴AH=FH=![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.



科目:初中数学 来源: 题型:
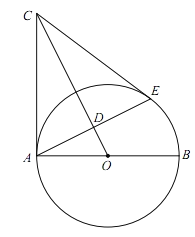
【题目】已知:如图,AB是⊙O的直径,点C是过点A的⊙O的切线上一点,连接OC,过点A作OC的垂线交OC于点D,交⊙O于点E,连接CE.
(1)求证:CE与⊙O相切;
(2)连结BD并延长交AC于点F,若OA=5,sin∠BAE=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鲁在一个不透明的盒子里装了5个除颜色外其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
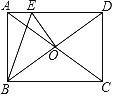
【题目】如图,矩形ABCD的对角线AC与BD交于点O,点E在AD上,且DE=CD,连接OE,∠ABE=![]() ∠ACB,若AE=2,则OE的长为_____.
∠ACB,若AE=2,则OE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为![]() ,两车之间的距离为)
,两车之间的距离为)![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系,根据图象进行探究:
之间的函数关系,根据图象进行探究:
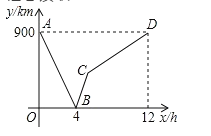
(1)甲、乙两地之间的距离为 ![]() ;
;
(2)请解释图中点![]() 的实际意义:__________;
的实际意义:__________;
(3)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,若CD=1,EH=3,求BE长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点O为坐标原点,直线![]() 交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且
交x轴于点A,交y轴于点B,点D在直线AB上,点D的纵坐标为6,点C在x轴上且位于原点右侧,连接CD,且![]() .
.

![]() 如图1,求直线CD的解析式;
如图1,求直线CD的解析式;
![]() 如图2,点P在线段AB上
如图2,点P在线段AB上![]() 点P不与点A,B重合
点P不与点A,B重合![]() ,过点P作
,过点P作![]() 轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
轴,交CD于点Q,点E是PQ的中点,设P点的横坐标为t,EQ的长为d,求d与t之间的函数关系式,并直接写出自变量t的取值范围;
![]() 如图3,在
如图3,在![]() 的条件下,以CQ为斜边作等腰直角
的条件下,以CQ为斜边作等腰直角![]() ,且点M在直线CD的右侧,连接OE,OM,当
,且点M在直线CD的右侧,连接OE,OM,当![]() 时,求点M的坐标.
时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
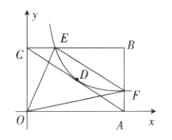
【题目】矩形OABC在平面直角坐标系中的位置如图所示,O为坐标原点,点B的坐标为(10,8),连接AC,已知反比例函数y=![]() (m≠0)在第一象限的图象经过矩形OABC的对角线的交点D,并交BC于点E,交AB于点F.
(m≠0)在第一象限的图象经过矩形OABC的对角线的交点D,并交BC于点E,交AB于点F.
(1)求线段AC所在直线的解析式和m的值.
(2)连接OE,OF,EF,求△OEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com