
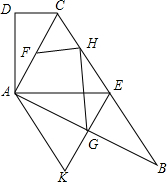
 如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.分析 (1)欲证明AC2=CD•BC,只需推知△ACD∽△BCA即可;
(2)①连接AH.构建直角△AHC,利用直角三角形斜边上的中线等于斜边的一半、等腰对等角以及等量代换得到:∠FHG=∠CAB=90°,即FH⊥GH;
②利用“在直角三角形中,30度角所对的直角边等于斜边的一半”、“直角三角形斜边上的中线等于斜边的一半”推知四边形AKEC的四条边都相等,则四边形AKEC是菱形.
解答  证明:(1)∵AC平分∠BCD,
证明:(1)∵AC平分∠BCD,
∴∠DCA=∠ACB.
又∵AC⊥AB,AD⊥AE,
∴∠DAC+∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.
又∵E是BC的中点,
∴AE=BE,
∴∠EAB=∠ABC,
∴∠DAC=∠ABC,
∴△ACD∽△BCA,
∴$\frac{AC}{BC}$=$\frac{CD}{AC}$,
∴AC2=CD•BC;
(2)①证明:连接AH.
∵∠ADC=∠BAC=90°,点H、D关于AC对称,
∴AH⊥BC.
∵EG⊥AB,AE=BE,
∴点G是AB的中点,
∴HG=AG,
∴∠GAH=GHA.
∵点F为AC的中点,
∴AF=FH,
∴∠HAF=∠FHA,
∴∠FHG=∠AHF+∠AHG=∠FAH+∠HAG=∠CAB=90°,
∴FH⊥GH;
②∵EK⊥AB,AC⊥AB,
∴EK∥AC,
又∵∠B=30°,
∴AC=$\frac{1}{2}$BC=EB=EC.
又EK=EB,
∴EK=AC,
即AK=KE=EC=CA,
∴四边形AKEC是菱形.
点评 本题考查了四边形综合题,需要熟练掌握相似三角形的判定与性质,“直角三角形斜边上的中线等于斜边的一半”、“在直角三角形中,30度角所对的直角边等于斜边的一半”以及菱形的判定才能解答该题,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年级 | 七年级 | 八年级 | 九年级 |
| 合格人数 | 270 | 262 | 254 |
| A. | 七年级的合格率最高 | B. | 八年级的学生人数为262名 | ||
| C. | 八年级的合格率高于全校的合格率 | D. | 九年级的合格人数最少 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
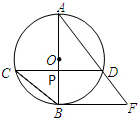 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
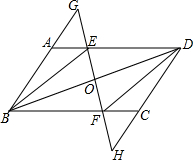 已知:如图,在?ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
已知:如图,在?ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
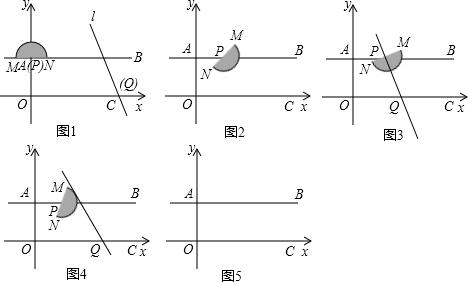
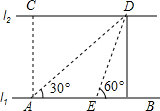 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )
如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com