
【题目】已知:如图(1),在△ABC中,AB=BC=2CD,∠ABC=∠DCB=120°,AC交BD于点E.

(1)如图1:作BM⊥CA于M,求证:△DCE≌△BME;
(2)如图2:点F为BC中点,连接AF交BD于点G,当AB=a时,求线段FG的长度(用含a的代数式表示);
(3)如图3:在(2)的条件下,将△ABG沿AG翻折得到△AKG,延长AK交BD于点H,若BH=5![]() ,求CE的长.
,求CE的长.
【答案】(1)见解析;(2)![]() a;(3)
a;(3)![]()
【解析】
(1)首先证明BC=2BM,可得CD=BM,根据AAS即可证明△DCE≌△BME;
(2)如图2中,作FN⊥AB交AB的延长线于N.解直角三角形求出AF,再利用相似三角形的性质求出FG;
(3)如图3中,作FN⊥AB交AB的延长线于N,BM⊥AC于M.设AB=a.解直角三角形求出GH,BG(用a表示),构建方程求出a即可解决问题.
解:(1)证明:如图1中,
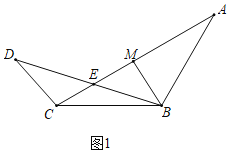
∵BC=BA,∠ABC=120°,
∴∠A=∠BCA=30°,
∵BM⊥AC,
∴∠BMC=90°,
∴BM=![]() BC,
BC,
∵BC=2CD,BC=2BM,
∴CD=BM,
∵∠BCD=120°,
∴∠ECD=∠EMB=90°,
∵∠DEC=∠BEM,
∴△DCE≌△BME(AAS).
(2)解:如图2中,作FN⊥AB交AB的延长线于N.
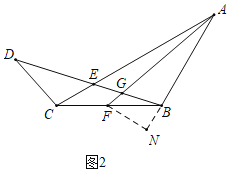
∵CF=BF,AB=BC=2CD,
∴CD=BF,
∵∠DCB=∠FBA=120°,CB=BA,
∴△DCB≌△FBA(SAS),
∴∠DBC=∠BAF,
∵∠BFG=∠BFA,
∴△FBG∽△FAB,
∴![]() =
=![]() ,
,
在Rt△BFN中,∵BF=![]() a,∠FBN=60°,∠N=90°,
a,∠FBN=60°,∠N=90°,
∴BN=![]() a,FN=
a,FN=![]() a,
a,
∴AF=![]() =
=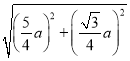 =
=![]() a,
a,
∴FG=![]() =
=![]() =
=![]() a.
a.
(3)解:如图3中,作FN⊥AB交AB的延长线于N,BM⊥AC于M.设AB=a.
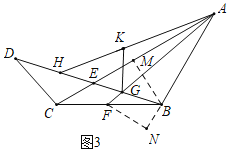
由(2)可知:FG=![]() a,
a,
∴AG=AF﹣FG=![]() a,
a,
∵△FBG∽△FAB,
∴![]() =
=![]()
BG=![]() =
=![]() a,
a,
∵△AKG和△ABG关于直线AG对称,
∴∠GAH=∠BAF,
∴∠DBC=∠GAH,
又∵∠BGF=∠AGH,
∴△BGF∽△AGH,
∴![]() =
=![]() ,
,
∴GH=![]() =
=![]() a,
a,
∵BH=BG+GH=![]() a=5
a=5![]() ,
,
∴a=14,
∴BC=AB=14,
∵BM⊥AC,
∴∠CMB=90°,
∴CM=BCcos30°=7![]() ,
,
∵△DEC≌△BEM,
∴EC=EM=![]() CM=
CM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.
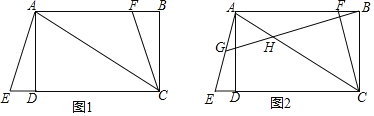
(1)若DE=1,CF=![]() ,求CD的长;
,求CD的长;
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=![]() AC.
AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
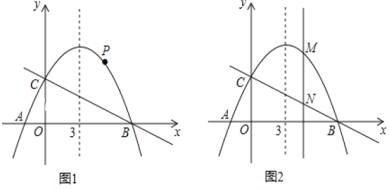
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 (m-1)x![]() -mx+1=0。
-mx+1=0。
(1)证明:不论m为何值时,方程总有实数根;
(2)若m为整数,当m为何值时,方程有两个不相等的整数根。
查看答案和解析>>
科目:初中数学 来源: 题型:
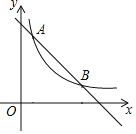
【题目】如图,在平面直角坐标系中,直线y=﹣kx+m与双曲线y=![]() (x>0)交于A、B两点,点A的横坐标为1,点B的纵坐标为2,点P是y轴上一动点,当△PAB的周长最小时,点P的坐标是_______.
(x>0)交于A、B两点,点A的横坐标为1,点B的纵坐标为2,点P是y轴上一动点,当△PAB的周长最小时,点P的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC,若∠BAC=45°.
(1)求证:OE=![]() BC;
BC;
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H,若BD=6,CD=4,求AD的长;
(3)作OM⊥AB于M,ON⊥AC于N,在(2)的条件下求![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点O作一条直线分别交DA,BC的延长线于点E,F,连接BE,DF.
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,![]() ,AE=2,求菱形ABCD的边长.
,AE=2,求菱形ABCD的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】HW公司2018年使用自主研发生产的“QL“系列甲、乙、丙三类芯片共2800万块,生产了2800万部手机,其中乙类芯片的产量是甲类芯片的2倍,丙类芯片的产量比甲,乙两类芯片产量的和还多400万块.这些“QL“芯片解决了该公司2018年生产的全部手机所需芯片的10%.
(1)求2018年甲类芯片的产量.
(2)HW公司计划2020年生产的手机全部使用自主研发的“QL”系列芯片.从2019年起逐年扩大“QL”芯片的产量,2019年、2020年这两年,甲类芯片每年的产量都比前一年增长一个相同的百分数m%,乙类芯片的产量平均每年增长的百分数比m%小1%,丙类芯片的产量每年按相同的数量3200万块递增.这样,2020年的HW公司的手机产量比2018年全年的手机产量多10%,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com