
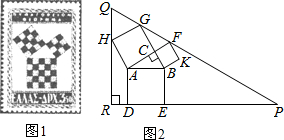
 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票图1所示.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图2的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,则RQ=7+2$\sqrt{3}$,△PQR的周长等于27+13$\sqrt{3}$.
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票图1所示.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图2的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,则RQ=7+2$\sqrt{3}$,△PQR的周长等于27+13$\sqrt{3}$. 分析 在直角△ABC中,根据三角函数即可求得AC,进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长,在直角△QRP中运用三角函数即可得到RP、QP的长,就可求出△PQR的周长.
解答  解:延长BA交QR于点M,连接AR,AP.
解:延长BA交QR于点M,连接AR,AP.
∵AC=GC,BC=FC,∠ACB=∠GCF,
∴△ABC≌△GFC,
∴∠CGF=∠BAC=30°,
∴∠HGQ=60°,
∵∠HAC=∠BAD=90°,
∴∠BAC+∠DAH=180°,
又∵AD∥QR,
∴∠RHA+∠DAH=180°,
∴∠RHA=∠BAC=30°,
∴∠QHG=60°,
∴∠Q=∠QHG=∠QGH=60°,
∴△QHG是等边三角形.
AC=AB•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
则QH=HA=HG=AC=2$\sqrt{3}$.
在直角△HMA中,HM=AH•sin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3.AM=HA•cos60°=$\sqrt{3}$.
在直角△AMR中,MR=AD=AB=4.
∴QR=2$\sqrt{3}$+3+4=7+2$\sqrt{3}$.
∴QP=2QR=14+4$\sqrt{3}$.
PR=QR•$\sqrt{3}$=7$\sqrt{3}$+6.
∴△PQR的周长等于RP+QP+QR=27+13$\sqrt{3}$.
故答案为:7+2$\sqrt{3}$;27+13$\sqrt{3}$.
点评 考查了勾股定理的证明和含30度角的直角三角形,正确运用三角函数以及勾股定理是解决本题的关键.


科目:初中数学 来源: 题型:解答题
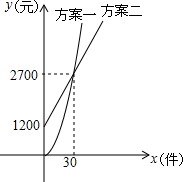 某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案一所示图形是顶点B在原点的抛物线的一部分,方案二所示图形是射线.设推销员推销产品的数量为x(件),付给推销员的月报酬为y(元).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
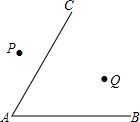 如图,已知∠BAC,用直尺和圆规作图:
如图,已知∠BAC,用直尺和圆规作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
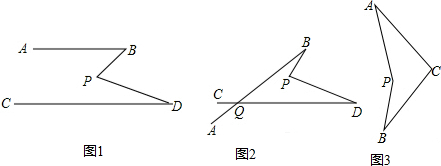
 已知,△ABC在平面直角坐标系中的位置如图所示.
已知,△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com