
【题目】图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.
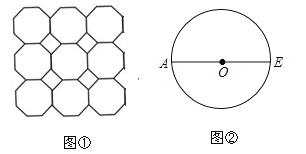
(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于 .
【答案】(1)作图见试题解析;(2)![]() .
.
【解析】
试题分析:(1)作AE的垂直平分线交⊙O于C,G,作∠AOG,∠EOG的角平分线,分别交⊙O于H,F,反向延长 FO,HO,分别交⊙O于D,B顺次连接A,B,C,D,E,F,G,H,八边形ABCDEFGH即为所求;
(2)由八边形ABCDEFGH是正八边形,求得∠AOD的度数,得到![]() 的长,设这个圆锥底面圆的半径为R,根据圆的周长的公式即可求得结论.
的长,设这个圆锥底面圆的半径为R,根据圆的周长的公式即可求得结论.
试题解析:(1)如图所示,八边形ABCDEFGH即为所求;

(2)∵八边形ABCDEFGH是正八边形,∴∠AOD=![]() ×3=135°,∵OA=5,∴
×3=135°,∵OA=5,∴![]() 的长=
的长=![]() =
=![]() ,设这个圆锥底面圆的半径为R,∴2πR=
,设这个圆锥底面圆的半径为R,∴2πR=![]() ,∴R=
,∴R=![]() ,即这个圆锥底面圆的半径为
,即这个圆锥底面圆的半径为![]() .故答案为:
.故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直且相等的四边形是正方形
D. 两条对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城际铁路的正式开通,从甲市经丙市到乙市的高铁里程比普快里程缩短了90km,运行时间减少了8h,已知甲市到乙市的普快列车里程为1220km.高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王先生要从甲市去距离大约780km的丙市参加14:00召开的会议,如果他买到当日9:20从甲市到丙市的高铁票,而且从丙市火车站到会议地点最多需要1小时.试问在高铁列车准点到达的情况下,它能否在开会之前20分钟赶到会议地点?
查看答案和解析>>
科目:初中数学 来源: 题型:
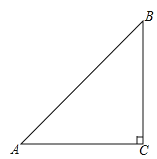
【题目】如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
(1)(4分)用尺规作图,在CA的延长线上截取AD=AB,并连接BD(不写作法,保留作图痕迹);
(2)(4分)求∠BDC的度数;
(3)(4分)定义:在直角三角形中,一个锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即![]() ,根据定义,利用图形求cot22.5°的值.
,根据定义,利用图形求cot22.5°的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里吨),铁路运价为1元/(公里吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.![]()
问:
(1)这家食品厂到A地的距离是多少?
(2)这家食品厂此次共买进原料和卖出食品各多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com