
分析 根据差倒数的定义分别求出前几个数便不难发现,每3个数为一个循环组依次循环,用2013除以3,根据余数的情况确定出与a2013相同的数即可得解.
解答 解:∵a1=-$\frac{1}{3}$,
∴a2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,
a3=$\frac{1}{1-\frac{3}{4}}$=4,
a4=$\frac{1}{1-4}$=-$\frac{1}{3}$,
…
2013÷3=671.
∴a2013与a3相同,为4.
故答案为:4.
点评 此题考查数字的变化规律,理解差倒数的定义并求出每3个数为一个循环组依次循环是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E
如图,等腰Rt△ABC中,∠ACB=90°,CA=CB,点D在AB上,AD=AC,BE⊥直线CD于E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
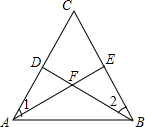 已知:如图,点D,E分别在△ABC的边AC和BC上,AE与BD相交于点F,给出下面四个条件:①∠1=∠2;②AD=BE;③AF=BF;④DF=EF,从这四个条件中选取两个,不能判定△ABC是等腰三角形的是( )
已知:如图,点D,E分别在△ABC的边AC和BC上,AE与BD相交于点F,给出下面四个条件:①∠1=∠2;②AD=BE;③AF=BF;④DF=EF,从这四个条件中选取两个,不能判定△ABC是等腰三角形的是( )| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
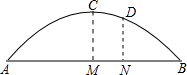 如图,一石拱桥呈抛物线状,已知石拱跨度AB为40米,拱高CM为16米,把桥拱看作一个二次函数的图象,建立适当的坐标系.
如图,一石拱桥呈抛物线状,已知石拱跨度AB为40米,拱高CM为16米,把桥拱看作一个二次函数的图象,建立适当的坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知数a,b,c的大小关系如图所示,则下列各式:
已知数a,b,c的大小关系如图所示,则下列各式:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com