
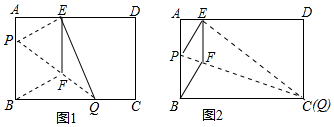
分析 (1)把B(-m,0)点坐标代入y=(m-$\frac{9}{2}$)x-2,求出m即可解决问题;
(2)如图1中,作EF⊥OB于F.根据S△BOE=$\frac{1}{2}$•OB•EF,即可解决问题;
(3)如图2中,作EN⊥OB于N,OH⊥BC于H.首先证明四边形OFBE是等腰梯形,推出∠F=∠EOF,由∠D=90°,∠F=∠EOF=∠OEH=45°,可得△OEH是等腰直角三角形,推出OH=EH,由$\frac{1}{2}$•OB•OC=$\frac{1}{2}$•BC•OH,可得OH=$\frac{OB•OC}{BC}$=$\frac{8}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$,在Rt△OHC中,HC=$\sqrt{O{C}^{2}-O{H}^{2}}$=$\frac{2\sqrt{5}}{5}$,推出EC=$\frac{6\sqrt{5}}{5}$,BE=$\frac{4\sqrt{5}}{5}$,由EN∥OC,可得$\frac{EN}{OC}$=$\frac{BN}{OB}$=$\frac{BE}{BC}$,求出EN、BN即可解决问题;
解答 解:(1)由题意B(-m,0),
∵一次函数y=(m-$\frac{9}{2}$)x-2经过B点,
∴0=(m-$\frac{9}{2}$)×(-m)-2,
解得m=4或$\frac{1}{2}$(舍弃).
∴m=4.
(2)如图1中,作EF⊥OB于F.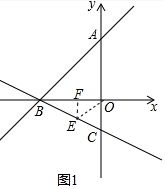
由(1)可知直线BC的解析式为y=-$\frac{1}{2}$x-2,B(-4,0),
∵E(t,-$\frac{1}{2}$t-2),
∴EF=$\frac{1}{2}$t+2,
∴S=$\frac{1}{2}$•OB•EF=$\frac{1}{2}$×4×($\frac{1}{2}$t+2)=t+4(-4<t≤0).
(3)如图2中,作EN⊥OB于N,OH⊥BC于H.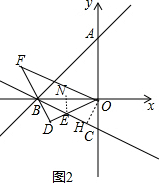
∵∠OBD+∠DEB-∠FOB=90°,∠OBD=∠F+∠FOB,
∴∠F+∠DEB=90°,∵∠DBE+∠DEB=90°,
∴∠F=∠DBE,
∴OF∥BC,
∵BF=OE,
∴四边形OFBE是等腰梯形,
∴∠F=∠EOF,∵∠D=90°,
∴∠F=∠EOF=∠OEH=45°,
∴△OEH是等腰直角三角形,
∴OH=EH,
∵$\frac{1}{2}$•OB•OC=$\frac{1}{2}$•BC•OH,
∴OH=$\frac{OB•OC}{BC}$=$\frac{8}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$,
在Rt△OHC中,HC=$\sqrt{O{C}^{2}-O{H}^{2}}$=$\frac{2\sqrt{5}}{5}$,
∴EC=$\frac{6\sqrt{5}}{5}$,BE=$\frac{4\sqrt{5}}{5}$,
∵EN∥OC,
∴$\frac{EN}{OC}$=$\frac{BN}{OB}$=$\frac{BE}{BC}$,
∴$\frac{EN}{2}$=$\frac{BN}{4}$=$\frac{\frac{4\sqrt{5}}{5}}{2\sqrt{5}}$,
∴EN=$\frac{4}{5}$,BN=$\frac{8}{5}$,
∴ON=OB-BN=$\frac{12}{5}$,
∴E(-$\frac{12}{5}$,-$\frac{4}{5}$).
点评 本题考查一次函数综合题、待定系数法、平行线分线段成比例定理、等腰梯形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用面积法求有关线段,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).
某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为2.4米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.2米,看台最低点A与旗杆底端D之间的距离为15米(C,A,D在同一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=ax+b与x轴交于A,与y轴交于B,与双曲线y=$\frac{k}{x}$交于点C,D,OA=2OB=2.△OAB与△OAD的面积相等.
如图,直线y=ax+b与x轴交于A,与y轴交于B,与双曲线y=$\frac{k}{x}$交于点C,D,OA=2OB=2.△OAB与△OAD的面积相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
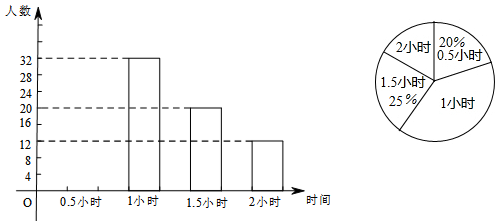
 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com