
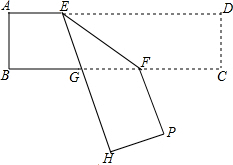
 如图所示,长方形纸条ABCD沿EF折叠后,∠EFB=35°,试求∠DEH与∠BGH的大小.
如图所示,长方形纸条ABCD沿EF折叠后,∠EFB=35°,试求∠DEH与∠BGH的大小. 科目:初中数学 来源: 题型:选择题
| A. | 3,5,9 | B. | 4,6,8 | C. | 1,$\sqrt{3}$,2 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解恒安新区每天的流动人口数,采用抽样调查方式 | |
| B. | 要了解全市七年级学生英语单词的掌握情况,采用全面调查方式 | |
| C. | 了解矿区居民日平均用水量,采用全面调查方式 | |
| D. | 旅客进火车站上车前的安检,采用抽样调查方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.105×109 | B. | 1.05×109 | C. | 1.05×108 | D. | 105×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com