
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动:同时点Q沿边AB,BC从点A开始向点C以acm/s的速度移动,当点P移动到点A时,P,Q同时停止移动.设点P出发x秒时,△PAQ的面积为ycm2,y与x的函数图象如图②,线段EF所在的直线对应的函数关系式为y=﹣4x+21,则a的值为( )
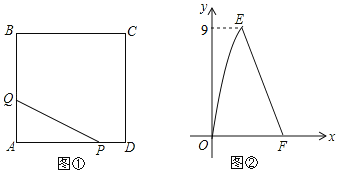
A. 1.5B. 2C. 3D. 4
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法中①abc<0;②2a+b=0;③当﹣1<x<3时,y>0;④2c﹣3b<0.正确的结论有( )
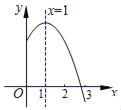
A. ①②B. ②③④C. ①③D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
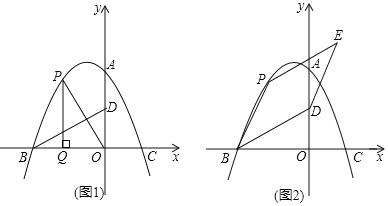
【题目】如图,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与y轴交于点A(0,8),与x轴交于B、C两点,其中点C的坐标为(4,0).点P(m,n)为该二次函数在第二象限内图象上的动点,点D的坐标为(0,4),连接BD.
x2+bx+c的图象与y轴交于点A(0,8),与x轴交于B、C两点,其中点C的坐标为(4,0).点P(m,n)为该二次函数在第二象限内图象上的动点,点D的坐标为(0,4),连接BD.
(1)求该二次函数的表达式及点B的坐标;
(2)连接OP,过点P作PQ⊥x轴于点Q,当以O、P、Q为顶点的三角形与△OBD相似时,求m的值;
(3)连接BP,以BD、BP为邻边作BDEP,直线PE交x轴于点T.当点E落在该二次函数图象上时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在﹣9,﹣6,﹣3,﹣1,2,3,6,8,11这九个数中,任取一个作为a值,能够使关于x的一元二次方程x2+ax+9=0有两个不相等的实数根的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级学生的数学作业完成情况,将完成情况分为四个等级:
等级 | A | B | C | D |
情况分类 | 好 | 较好 | 一般 | 不好 |
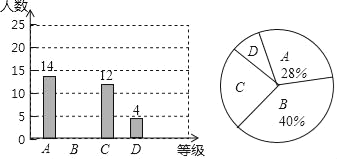
随机对该年级若干名学生进行了调查,然后把调查结果绘制成两幅不完整的统计图.请根据图中的信息解答下列问题:
(1)补全条形统计图;
(2)该年级共有700人,估计该年级数学作业完成等级为D等的人数;
(3)在此次调查中,有甲、乙、丙、丁四个班的学生数学作业完成表现出色,现决定从这四个班中随机选取两个班在全校举行一次数学作业展览,请用画树状图或列表的方法,求恰好选到甲、乙两个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
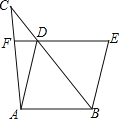
【题目】如图,在△ABC中,点D在BC边上,BC=3CD,分别过点B,D作AD,AB的平行线,并交于点E,且ED交AC于点F,AD=3DF.
(1)求证:△CFD∽△CAB;
(2)求证:四边形ABED为菱形;
(3)若DF=![]() ,BC=9,求四边形ABED的面积.
,BC=9,求四边形ABED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
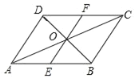
【题目】如图所示,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O作EF∥BC,EF与AB、CD分别相交于点E、F,则△DOF的面积与△BOA的面积之比为( )
A. 1:2B. 1:4C. 1:8D. 1:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,则下面说法正确的是( )
A. 1一定不是方程x2+bx+a=0的根B. 0一定不是方程x2+bx+a=0的根
C. ﹣1可能是方程x2+bx+a=0的根D. 1和﹣1都是方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
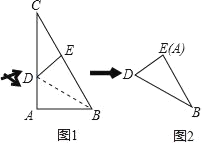
【题目】在三角形纸片ABC中,∠A=90°,∠C=30°,AC=10cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com