
【题目】如图,AB是⊙O的直径,点P是AB上一点,且点P是弦CD的中点.
(1)依题意画出弦CD,并说明画图的依据;(不写画法,保留画图痕迹)
(2)若AP=2,CD=8,求⊙O的半径.
【答案】(1)画图见解析,依据:平分弦(非直径)的直径垂直于弦;(2)⊙O的半径为5.
【解析】
(1)过P点作AB的垂线即可,作图依据是垂径定理的推论.
(2)设⊙O的半径为r,在Rt△OPD中,利用勾股定理构建方程即可解决问题.
(1)过P点作AB的垂线交圆与C、D两点, CD就是所求的弦,如图.
依据:平分弦(非直径)的直径垂直于弦;
(2)如图,连接OD,
∵OA⊥CD于点P,AB是⊙O的直径,
∴∠OPD=90°,PD=![]() CD,
CD,
∵CD=8,
∴PD=4.
设⊙O的半径为r,则OD=r,OP=OA﹣AP=r﹣2,
在Rt△ODP中,∠OPD=90°,
∴OD2=OP2+PD2,
即r2=(r﹣2)2+42,
解得r=5,
即⊙O的半径为5.


科目:初中数学 来源: 题型:
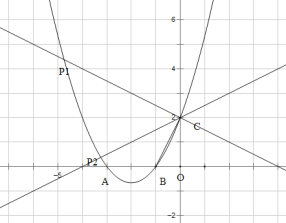
【题目】已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式.
(2)连接BC,求∠BCO的余切值.
(3)如果过点C的直线,交x轴于点E,交抛物线于点P,且∠CEO =∠BCO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
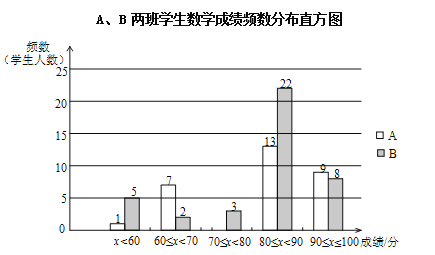
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,回答下列问题:
(1)补全数学成绩频数分布直方图;
(2)写出表中m、n的值;
(3)请你对比分析A、B两班学生的数学学习情况(至少从两个不同的角度分析).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
学习函数知识后,对于一些特殊的不等式,我们可以借助函数图象来求出它的解集,例如求不等式x﹣3>![]() 的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=
的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=![]() 的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>
的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>![]() 的解集为﹣1<x<0,或x>4.
的解集为﹣1<x<0,或x>4.
小东根据学习以上知识的经验,对求不等式x3+3x2﹣x﹣3>0的解集进行了探究.下面是小东的探究过程,请补充完整:
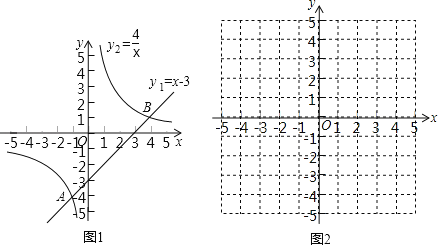
(1)将不等式按条件进行转化:当x=0时,原不等式不成立;x>0时,原不等式转化为x2+3x﹣1>![]() ;当x<0时,原不等式转化为______;
;当x<0时,原不等式转化为______;
(2)构造函数,画出图象:设y3=x2+3x﹣1,y4=![]() ,在同一坐标系(图2)中分别画出这两个函数的图象.
,在同一坐标系(图2)中分别画出这两个函数的图象.
(3)借助图象,写出解集:观察所画两个函数的图象,确定两个函数图象交点的横坐标,结合(1)的讨论结果,可知:不等式x3+3x2﹣x﹣3>0的解集为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
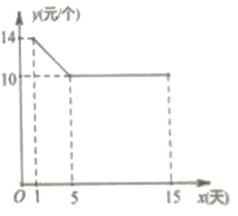
【题目】每年九月开学前后是文具盒的销售旺季,商场专门设置了文具盒专柜李经理记录了![]() 天的销售数量和销售单价,其中销售单价
天的销售数量和销售单价,其中销售单价![]() (元/个)与时间第
(元/个)与时间第![]() 天(
天(![]() 为整数)的数量关系如图所示,日销量
为整数)的数量关系如图所示,日销量![]() (个)与时间第
(个)与时间第![]() 天(
天(![]() 为整数)的函数关系式为:
为整数)的函数关系式为: 
![]() 直接写出
直接写出![]() 与
与![]() 的函数关系式,并注明自变量
的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
![]() 设日销售额为
设日销售额为![]() (元) ,求
(元) ,求![]() (元)关于
(元)关于![]() (天)的函数解析式;在这
(天)的函数解析式;在这![]() 天中,哪一天销售额
天中,哪一天销售额![]() (元)达到最大,最大销售额是多少元;
(元)达到最大,最大销售额是多少元;
![]() 由于需要进货成本和人员工资等各种开支,如果每天的营业额低于
由于需要进货成本和人员工资等各种开支,如果每天的营业额低于![]() 元,文具盒专柜将亏损,直接写出哪几天文具盒专柜处于亏损状态
元,文具盒专柜将亏损,直接写出哪几天文具盒专柜处于亏损状态
查看答案和解析>>
科目:初中数学 来源: 题型:
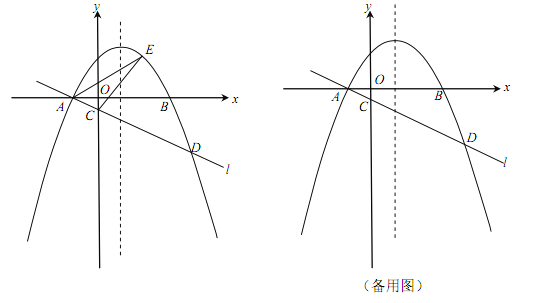
【题目】(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线![]() (
(![]() )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:![]() 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
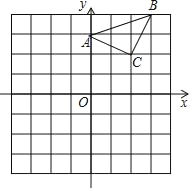
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com