
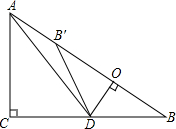
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.分析 (1)由∠DOB=∠ACB=90°,∠B=∠B,容易证明△DOB∽△ACB;
(2)先由勾股定理求出AB,由角平分线的性质得出DC=DO,再由HL证明Rt△ACD≌Rt△AOD,得出AC=AO,设BD=x,则DC=DO=8-x,由勾股定理得出方程,解方程即可.
解答 解:(1)∵DO⊥AB,
∴∠DOB=90°,
∴∠ACB=∠DOB,又∠B=∠B,
∴△DOB∽△ACB;
(2)∵∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AD平分∠CAB,DC⊥AC,DO⊥AB,
∴DC=DO,
在Rt△ACD和Rt△AOD中,
∵$\left\{\begin{array}{l}{AD=AD}\\{DC=DO}\end{array}\right.$,
∴Rt△ACD≌Rt△AOD(HL),
∴AC=AO=6,
设BD=x,则DC=DO=8-x,OB=AB-AO=4,
在Rt△BOD中,根据勾股定理得:DO2+OB2=BD2,
即(8-x)2+42=x2,
解得:x=5.
点评 本题考查了相似三角形的判定与性质、勾股定理、全等三角形的判定与性质、角平分线的性质等知识;根据题意列出方程,解方程才能得出结果.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
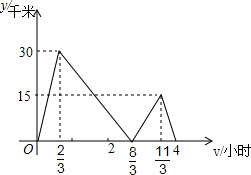 甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留)前往终点B地,甲、乙两车之间的距离y(千米)与甲车行驶时间t(小时)之间的函数关系如图所示.小红通过图象得出4个信息:
甲、乙两车沿同一平直公路由A地匀速行驶(中途不停留)前往终点B地,甲、乙两车之间的距离y(千米)与甲车行驶时间t(小时)之间的函数关系如图所示.小红通过图象得出4个信息:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com