
【题目】如图,已知在△ABC中,AB=AC.
(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
科目:初中数学 来源: 题型:
【题目】某校九年级在开展“学会感恩“的活动月中,对九年级(2)班40人一周内(周一至周五)零花钱的使用情况进行调查,结果如下表:
人数 | 5 | 15 | 13 | 7 |
使用零花钱(单位:元) | 15 | 20 | 30 | 35 |
那么学生使用零花钱的中位数和众数分别是( )
A. 15和35 B. 20和20 C. 15和20 D. 20和25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为筹备班级的元旦联欢会,班长对全班同学爱吃哪几种零食作民意调查,从而最终决定买什么零食,下列调查数据中最值得关注的是( )
A. 中位数B. 平均数C. 众数D. 标准差
查看答案和解析>>
科目:初中数学 来源: 题型:
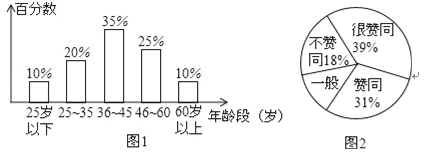
【题目】据报载,在“百万家庭低碳行,垃圾分类要先行”活动中,某地区对随机抽取的1000名公民的年龄段分布情况和对垃圾分类所持态度进行调查,并将调查结果分别绘成条形图(图1)、扇形图(图2).
(1)图2中所缺少的百分数是 ;
(2)这次随机调查中,如果公民年龄的中位数是正整数,那么这个中位数所在年龄段是 ____ (填写年龄段);
(3)这次随机调查中,年龄段是“25岁以下”的公民中“不赞成”的有5名,它占“25岁以下”人数的百分数是 ___ ;
(4)如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有 ____名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.

(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图像反映的过程是:甲乙两人同时从![]() 地出发,以各自的速度匀速向
地出发,以各自的速度匀速向![]() 地行驶,甲先到
地行驶,甲先到![]() 地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为
地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为![]() ,
, ![]() 表示甲乙两人相距的距离,
表示甲乙两人相距的距离, ![]() 表示乙行驶的时间.现有以下
表示乙行驶的时间.现有以下![]() 个结论:①
个结论:①![]() 、
、![]() 两地相距
两地相距![]() ;②点
;②点![]() 的坐标为
的坐标为![]() ;③甲去时的速度为
;③甲去时的速度为![]() ;④甲返回的速度是
;④甲返回的速度是![]() .以上
.以上![]() 个结论中正确的是_______________.
个结论中正确的是_______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com