
 如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B,C三点,且AB=4,点D(2,$\frac{3}{2}$)在抛物线上,直线l是一次函数y=kx-2(k≠0)的图象,点O是坐标原点.
如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B,C三点,且AB=4,点D(2,$\frac{3}{2}$)在抛物线上,直线l是一次函数y=kx-2(k≠0)的图象,点O是坐标原点.分析 (1)由抛物线的对称轴为x=1,AB=4,可求出A、B两点的横坐标,从而可将抛物线的解析式设成交点式,然后把点D的坐标代入抛物线的解析式就可解决问题;
(2)根据抛物线的解析式可求出点C的坐标,从而得到CD∥x轴,CD=2,进而可求出四边形OBDC的面积,设直线y=kx-2与CD、x轴分别交于点E、F,然后用k的代数式表示点E、F的横坐标,然后根据条件“直线l平分四边形OBDC的面积”,建立关于k的方程,就可求出k的值.
解答 解:(1)∵抛物线的对称轴为x=1,AB=4,
∴xA=1-$\frac{4}{2}$=-1,xB=1+$\frac{4}{2}$=3.
则抛物线的解析式可设为y=a(x+1)(x-3).
∵点D(2,$\frac{3}{2}$)在抛物线上,
∴$\frac{3}{2}$=a(2+1)(2-3),
解得:a=-$\frac{1}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$(x+1)(x-3),即y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$;
(2)设直线y=kx-2与CD、x轴分别交于点E、F,如图所示.
由xC=0得yC=$\frac{3}{2}$,则点C的坐标为(0,$\frac{3}{2}$).
∵D(2,$\frac{3}{2}$),∴CD∥x轴,CD=2,
∴S四边形OBDC=$\frac{1}{2}$×(2+3)×$\frac{3}{2}$=$\frac{15}{4}$.
由yE=$\frac{3}{2}$得xE=$\frac{7}{2k}$,由yF=0得xF=$\frac{2}{k}$,
∴S四边形OFEC=$\frac{1}{2}$×($\frac{2}{k}$+$\frac{7}{2k}$)×$\frac{3}{2}$=$\frac{1}{2}$×$\frac{15}{4}$,
解得:k=$\frac{33}{15}$.
点评 本题主要考查了抛物线的轴对称性、抛物线的交点式、直线上点的坐标特征等知识,抛物线的解析式通常有三种形式:一般形式y=ax2+bx+c(a≠0),顶点式y=a(x-h)2+k(a≠0),(其中顶点坐标为(h,k)),交点式为y=a(x-x1)(x-x2)(a≠0),(其中抛物线与x轴的交点坐标分别为(x1,0),(x2,0)),应灵活应用.


科目:初中数学 来源: 题型:选择题
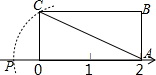 如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )
如图,长方形OABC放在数轴上,OA=2,OC=1,以A为圆心,AC长为半径画弧交数轴于P点,则P点表示的数为( )| A. | 2-$\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{5}-2$ | D. | $\sqrt{5}-3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
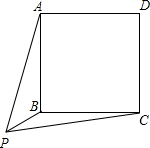 点P是正方形ABCD外一点,PB=12cm,△APB的面积是90cm2,△CPB的面积是48cm2.请你回答:正方形ABCD的面积是多少cm2?
点P是正方形ABCD外一点,PB=12cm,△APB的面积是90cm2,△CPB的面积是48cm2.请你回答:正方形ABCD的面积是多少cm2?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com