
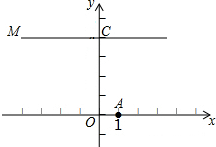 如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD.
如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD.分析 (1)将点A的坐标代入代入直线的解析式求得b的值,从而得到直线的解析式为y=-x+1,然后将y=4代入可求得点D的坐标;
(2)可分为DO=DP、DO=OP、DP=OP三种情况分类计算;
(3)根据(2)中三种情况可确定出d和r的值,然后由两圆内切可知:d=R-r,从而可求得R的值.
解答 解:(1)将x=1,y=0代入直线的解析式得:-1+b=0,
解得:b=1.
∴直线的解析式为y=-x+1.
将y=4代入y=-x+1得:-x+1=4,解得:x=-3.
∴点D的坐标为(-3,4).
(2)①如图1所示:DO=OP.
在△OCD中,由勾股定理得:OD=$\sqrt{D{C}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5. ,
,
OP=OD=5.
∴点P的坐标为(-5,0).
②如图2所示:PD=DO.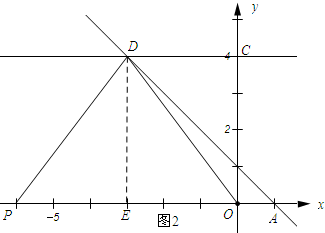
过点D作DE⊥x轴,垂足为E.
∵DP=PO,DE⊥OP,
∴PE=OE.
∴OP=2OP=2×3=6.
∴点P的坐标为(-6,0).
③如图3所示:DP=OP.过点P作PE⊥DO,垂足为E,过点E作EF⊥OP垂足为F.
∵PD=PO,PE⊥DO,
∴ED=OE.
∴点E的坐标为(-1.5,2).
∵∠EOF+∠FEO=90°,∠EPO+∠EOF=90°,
∴∠EPO=∠OEF.
又∵∠PFE=∠EFO,
∴△EFP∽△OFE.
∴$\frac{EF}{PF}=\frac{OF}{EF}$.
∴PF=$\frac{E{F}^{2}}{OF}$=$\frac{4}{\frac{3}{2}}$=$\frac{8}{3}$.
∴OP=$\frac{3}{2}$+$\frac{8}{3}$=$\frac{25}{6}$.
∴点P的坐标为(-$\frac{25}{6}$,0).
综上所述,点P的坐标为(-5,0)或(-6,0)或(-$\frac{25}{4}$,0).
(3)∵以P点为圆心,PD为半径的圆与圆O内切,
∴d=R-r.
①当DO=OP=5时,如图4所示:过点D作DE⊥OP,垂足为E.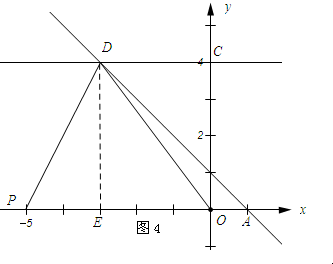
r=PD=$\sqrt{P{E}^{2}+E{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,d=PO=5.
∴R=d+r=5+2$\sqrt{5}$.,
②如图5所示:PD=DO=5时.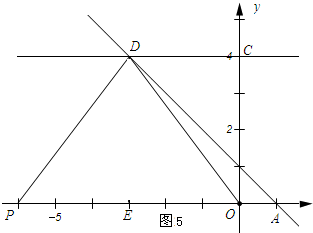
∵r=PD=5,d=OP=6,
∴R=5+6=11.
③如图6所示:当DP=OP=$\frac{25}{6}$时.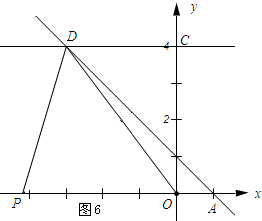
d=r=$\frac{25}{4}$.
∴R=$\frac{25}{2}$.
综上所述圆O的半径为5$+2\sqrt{5}$或11或$\frac{25}{2}$.
点评 本题主要考查的是圆和圆的位置关系、勾股定理的应用、等腰三角形的性质、待定系数法求一次函数的解析式,分类讨论是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
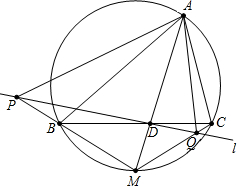 如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )
如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )| A. | 无论直线l的位置如何,总有直线PM与△ABD的外接圆相切 | |
| B. | 无论直线l的位置如何,总有∠PAQ>∠BAC | |
| C. | 直线l选取适当的位置,可使A、P、M、Q四点共圆 | |
| D. | 直线l选取适当的位置,可使S△APQ<S△ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
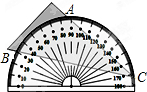 如图,三角形纸板放置在量角器上,三角形的顶点点C恰在半圆上,两边与半圆的交点记为A、B,A点的读数为80°,B点的读数为30°,则∠ACB的大小为25°.
如图,三角形纸板放置在量角器上,三角形的顶点点C恰在半圆上,两边与半圆的交点记为A、B,A点的读数为80°,B点的读数为30°,则∠ACB的大小为25°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
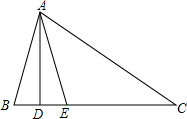 如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com