
 ),点M关于x轴的对称点为M′(0,-
),点M关于x轴的对称点为M′(0,- ),点A关于抛物线对称轴x=3的对称点为A'(6,3),连接A'M',根据轴对称性及两点间线段最短可知,A'M'的长就是所求点P运动的最短总路径的长,根据待定系数法可求出直线A'M'的解析式为y=
),点A关于抛物线对称轴x=3的对称点为A'(6,3),连接A'M',根据轴对称性及两点间线段最短可知,A'M'的长就是所求点P运动的最短总路径的长,根据待定系数法可求出直线A'M'的解析式为y= x-
x- ,从而求出E、F两点的坐标,再根据勾股定理可以求出A'M'=
,从而求出E、F两点的坐标,再根据勾股定理可以求出A'M'=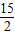 ,也就求出了最短总路径的长.
,也就求出了最短总路径的长.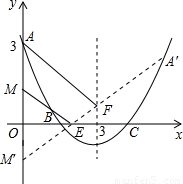 解:(1)根据题意,c=3,
解:(1)根据题意,c=3,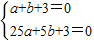
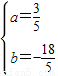
 x2-
x2-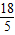 x+3.
x+3. x+1;(3分)
x+1;(3分) x+2.(4分)
x+2.(4分) ).
). ),
), x-
x- .
. ).(7分)
).(7分)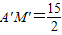 .
.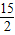 .(8分)
.(8分)

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(10)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(10)(解析版) 题型:解答题
 的值;
的值; 时,求抛物线和直线BE的解析式.
时,求抛物线和直线BE的解析式.
查看答案和解析>>
科目:初中数学 来源:2010年北京市密云县中考数学二模试卷(解析版) 题型:解答题
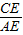 的值;
的值; 时,求抛物线和直线BE的解析式.
时,求抛物线和直线BE的解析式.
查看答案和解析>>
科目:初中数学 来源:2006年北京市中考数学试卷(课标卷)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com