
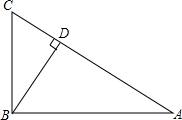
 如图,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,已知BC=5厘米,AC=13厘米.求:
如图,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,已知BC=5厘米,AC=13厘米.求:分析 根据勾股定理可求AB;
(1)将数值代入可求$\frac{AB}{BC}$;
(2)根据三角形面积公式可求BD,将数值代入可求$\frac{BD}{AC}$;
(3)根据比例线段的定义,找到和AB、BC构成比例线段的两条线段.
解答 解:在Rt△ABC中,∠ABC=90°,BC=5厘米,AC=13厘米,
AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=12厘米.
(1)$\frac{AB}{BC}$=$\frac{12}{5}$;
(2)在Rt△ABC中,$\frac{1}{2}$AC•BD=$\frac{1}{2}$AB•BC,BD=$\frac{60}{13}$,
$\frac{BD}{AC}$=$\frac{\frac{60}{13}}{13}$=$\frac{60}{169}$;
(3)∵AB:AC=BD:BC,
∴和AB、BC构成比例线段的两条线段是AC,BD.
点评 考查了比例线段,判定四条线段是否成比例,只要把四条线段按大小顺序排列好,判断前两条线段之比与后两条线段之比是否相等即可,求线段之比时,要先统一线段的长度单位,最后的结果与所选取的单位无关系.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
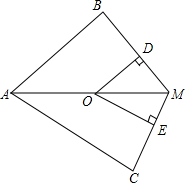 如图,已知AM平分∠BAC,点O是M上一点,OD⊥BM于点D,OE⊥CM于点E
如图,已知AM平分∠BAC,点O是M上一点,OD⊥BM于点D,OE⊥CM于点E查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com