
分析 先求出米老鼠早到的时间,再利用唐老鸭第n次发出指令浪费米老鼠的时间为1+$\frac{100n×10%}{100}$=1+0.1n,当n.次取数为1、2、3、4…15时,米老鼠浪费时间为27分>25分,所以唐老鸭要想获胜,必须使米老鼠浪费的时间超过25分钟,因此唐老鸭通过遥控器至少要发15次指令才能在比赛中获胜.
解答 解:米老鼠跑完全程用的时间为:10000÷100=100(分),
唐老鸭跑完全程的时间为:10000÷80=125(分),
米老鼠早到125-100=25(分),
唐老鸭第n次发出指令浪费米老鼠的时间为:1+$\frac{100n×10%}{100}$=1+0.1n.
当n次取数为1、2、3、4…15时,米老鼠浪费时间为1.1+1.2+1.3+1.4+…+2.3+2.4+2.5=27分>25分.
所以唐老鸭要想获胜,必须使米老鼠浪费的时间超过25分钟,因此唐老鸭通过遥控器至少要发15次指令才能在比赛中获胜.
答:如果唐老鸭想在比赛中获胜,那么它通过遥控器发出指令的次数至少应是15次.
点评 本题主要考查了有理数的应用题,解题的关键是正确的列出明确唐老鸭要想获胜,必须使米老鼠浪费的时间超过25分钟.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
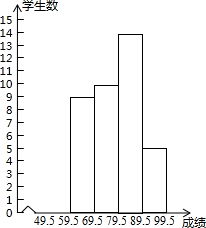 某班九年级(1)班40名学生期中考试的数学成绩(满分:100分)如下:
某班九年级(1)班40名学生期中考试的数学成绩(满分:100分)如下:| 63 | 84 | 91 | 53 | 69 | 81 | 61 | 69 | 91 | 78 |
| 75 | 81 | 80 | 67 | 76 | 81 | 79 | 94 | 61 | 69 |
| 89 | 70 | 70 | 87 | 81 | 86 | 90 | 88 | 85 | 67 |
| 71 | 82 | 87 | 75 | 87 | 95 | 53 | 65 | 74 | 77 |
| 成绩表 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
| 频数记录 |  | 正 | 正正 | 正正 | 正 |
| 频数 | 2 | 9 | 14 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 所挂物体的质量m(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度l(cm) | 15 | 18 | 21 | 24 | 27 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,
已知:如图,在△ABC中,AB=AC,点D、E分别在AB、AC上,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com