
分析 (1)根据加法交换律和加法结合律,求出算式的值是多少即可.
(2)首先计算括号里面的运算和乘方,然后计算乘除法,最后计算减法,求出算式的值是多少即可.
(3)首先计算括号里面的运算和乘方,然后计算减法,求出算式的值是多少即可.
解答 解:(1)($\frac{6}{7}$-1$\frac{1}{3}$)-(-1$\frac{1}{7}$+$\frac{5}{6}$)
=($\frac{6}{7}$+1$\frac{1}{7}$)-(1$\frac{1}{3}$+$\frac{5}{6}$)
=2-2$\frac{1}{6}$
=-$\frac{1}{6}$
(2)|-$\frac{7}{9}$|÷($\frac{2}{3}$-$\frac{1}{5}$)-$\frac{1}{3}$×(-4)2
=$\frac{7}{9}$÷$\frac{7}{15}$-$\frac{1}{3}$×16
=$\frac{5}{3}$-$\frac{16}{3}$
=-$\frac{11}{3}$
(3)-22-[-$\frac{1}{4}$+(1-$\frac{1}{5}$×0.6)÷(-2)2]
=-4-(-$\frac{1}{4}$+$\frac{22}{25}$÷4)
=-4-$\frac{3}{100}$
=-4$\frac{3}{100}$
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | 21-14$\sqrt{2}$ | B. | 21+14$\sqrt{2}$ | C. | 21+14$\sqrt{2}$或21-14$\sqrt{2}$ | D. | 3+2$\sqrt{2}$或21+14$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
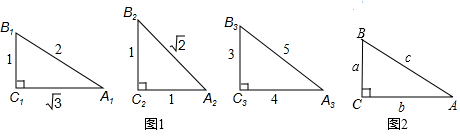
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
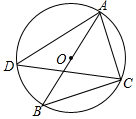 如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )
如图,⊙O的直径AB=2,点C、D在⊙O上,∠ADC=30°,则BC的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
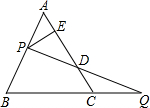 如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.
如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
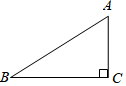 如图,在△ABC中,∠C=90°,AB=5,AC=2,则sinB的值是( )
如图,在△ABC中,∠C=90°,AB=5,AC=2,则sinB的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com