
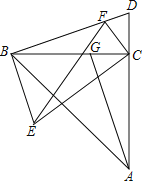
【题目】如图所示,在△ABD中,BC为AD边上的高线,tan∠BAD=1,在BC上截取CG=CD,连结AG,将△ACG绕点C旋转,使点G落在BD边上的F处,A落在E处,连结BE,若AD=4,tanD=3,则△CFD和△ECF的面积比为___;BE长为____.
【答案】1:5, ![]() .
.
【解析】
作CM⊥DF于M,则∠CMD=90°,由已知得出∠BCD=∠ACB=90°,AC=BC,BC=3CD,求出CD=1,AC=BC=3,证明△CDM∽△BDC,![]() ,得出
,得出![]() ,证明△AGC≌△BDC,得出∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,得出△CDF的面积=2△CDM的面积,求出△CFD的面积:△ECF的面积=1:5;证明△ACN≌△BCF,得出AN=BF,CN=CF=CD=CG=1,GN=DF,证明△CGN∽△CBE,得出
,证明△AGC≌△BDC,得出∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,得出△CDF的面积=2△CDM的面积,求出△CFD的面积:△ECF的面积=1:5;证明△ACN≌△BCF,得出AN=BF,CN=CF=CD=CG=1,GN=DF,证明△CGN∽△CBE,得出![]() ,在Rt△DCM中,求出DM=
,在Rt△DCM中,求出DM=![]() ,得出DF=2DM=
,得出DF=2DM=![]() ,代入计算即可.
,代入计算即可.
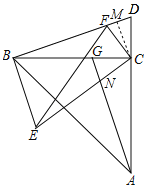
作CM⊥DF于M,如图所示:
则∠CMD=90°,
∵在△ABD中,BC为AD边上的高线,tan∠BAD=1,
∴∠BCD=∠ACB=90°,AC=BC,
在Rt△BCD中,∵tanD=3=![]() ,
,
∴BC=3CD,
∵AD=AC+CD=BC+CD=4,
∴CD=1,AC=BC=3,
∵∠CMD=∠BCD,∠D=∠D,
∴△CDM∽△BDC, ![]() ,
,
∴![]() ,
,
在△AGC和△BDC中,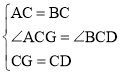 ,
,
∴△AGC≌△BDC(SAS),
∴∠CAG=∠CBD,△AGC的面积=△BDC的面积,∠CAG=∠CBD,
由旋转的性质得:CF=CD,EC=AC=BC,∠CEF=∠CAG,∠BCF=∠ACN,
∴△CDF的面积=2△CDM的面积,
∴△CFD的面积:△ECF的面积=1:5;
∵CG=CD,
∴CG=CF,
在△ACN和△BCF中,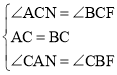 ,
,
∴△ACN≌△BCF(ASA),
∴AN=BF,CN=CF=CD=CG=1,
∴GN=DF,BC:CG=CE:CN,
∵∠GCN=∠BCE,
∴△CGN∽△CBE,
∴![]() ,
,
在Rt△DCM中,tanD=3,CD=1,
∴DM=![]() ,
,
∵CD=CF,CM⊥DF,
∴DF=2DM=![]() ,
,
∴GN=![]() ,
,
∴![]() =
=![]() ,
,
解得:BE=![]() ;
;
故答案为:1:5,![]() .
.


科目:初中数学 来源: 题型:
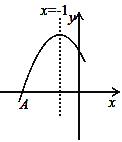
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论:①abc<0 ②b2﹣4ac>0 ③4b+c<0 ④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
,y2)为函数图象上的两点,则y1>y2⑤当﹣3≤x≤1时,y≥0,
其中正确的结论是(填写代表正确结论的序号)__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.
(1)另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c的数是一组勾股数.
(2)然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
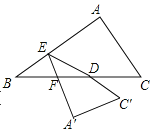
【题目】如图,在Rt△ABC中,AC=3,AB=4,D为斜边BC的中点,E为AB上一个动点,将△ABC沿直线DE折叠,A,C的对应点分别为![]() ,
,![]() ,
,![]() 交BC于点F,若△BEF为直角三角形,则BE的长度为______.
交BC于点F,若△BEF为直角三角形,则BE的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0),过(1,y1)、(2,y2).下列结论:①若y1>0时,则a+b+c>0; ②若a=2b时,则y1<y2;③若y1<0,y2>0,且a+b<0,则a>0.其中正确的结论个数为( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,
(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.
(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.
(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A点,已知﹣1<h<1,请求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是【 】
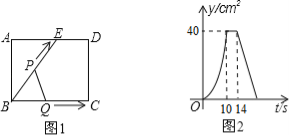
A.AE=6cm B.![]()
C.当0<t≤10时,![]() D.当t=12s时,△PBQ是等腰三角形
D.当t=12s时,△PBQ是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起市民与政府的高度关注,当市场猪肉的平均价格达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%,某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉,并规定其销售价格在5月20日每千克40元的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
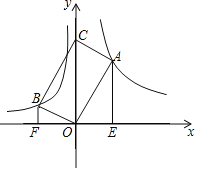
【题目】如图,点A、B在x轴的上方,∠AOB=90°,OA、OB分别与函数![]() 、
、![]() 的图象交于A、B两点,以OA、OB为邻边作矩形AOBC.当点C在y轴上时,分别过点A和点B作AE⊥x轴,BF⊥x轴,垂足分别为E、F,则
的图象交于A、B两点,以OA、OB为邻边作矩形AOBC.当点C在y轴上时,分别过点A和点B作AE⊥x轴,BF⊥x轴,垂足分别为E、F,则![]() =_______.
=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com