
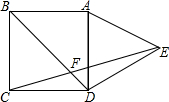
 如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
分析 由于四边形ABCD是正方形,△ADE是正三角形,由此可以得到CD=DE,接着利用正方形和正三角形的内角的性质即可求解.
解答 解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
又∵△ADE是正三角形,
∴CD=DE,∠ADE=60°,
∴△CDE是等腰三角形,∠CDE=90°+60°=150°,
∴∠ECD=∠DEC=15°,
∵∠BDC=45°,
∴∠CFD=180°-15°-45°=120°,
∴∠BFC=60°,
故选D
点评 此题主要考查了正方形和等边三角形的性质,同时也利用了三角形的内角和,解题首先利用正方形和等边三角形的性质证明等腰三角形,然后利用等腰三角形的性质即可解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
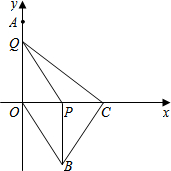 如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P运动的时间为t(0<t<4)秒.
如图,在平面直角坐标系中,点A (0,4).动点P从原点O出发,沿x轴正方向以每秒2个单位的速度运动,同时动点Q从点A出发,沿y轴负方向以每秒1个单位的速度运动,以QO、QP为邻边构造平行四边形OQPB,在线段OP的延长线长取点C,使得PC=2,连接BC、CQ.设点P运动的时间为t(0<t<4)秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=40,b=50,c=60 | B. | a=7,b=24,c=25 | C. | a=$\sqrt{41}$,b=4,c=5 | D. | a=$\frac{5}{4}$,b=1,c=$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
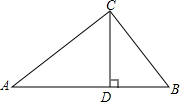 已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.
已知:如图,△ABC中,CD⊥AB于D点,AC=4,BC=3,DB=$\frac{9}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
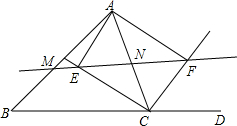 已知,如图,△ABC中,CE、CF分别是∠ACB和它的邻补角∠ACD的平分线,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
已知,如图,△ABC中,CE、CF分别是∠ACB和它的邻补角∠ACD的平分线,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com