
����Ŀ������ѧ̽�����ϣ���ʦ��ʾ��������̽�����⣬����һ����̽������֪��C���߶�AB����ƽ��������һ�㣬�ֱ���AC��BCΪ�ߣ���ABͬ�����ȱ���ACE����BCD������AD��BE���ڵ�P��
��1����ͼ1������C���߶�AB���ƶ�ʱ���߶�AD ��BE��������ϵ�� ��
��2����ͼ2������C��ֱ��AB�⣬�ҡ�ACB��120�㣬����Ľ����Ƿ�������������֤����������˵�����ɣ�
��3����ͼ3���ڣ�2���������£���ABΪ����AB��һ�����ȱ������Ρ�ABF������AD��BE��CF���ڵ�P����֤��PB+PC+PA=BE��
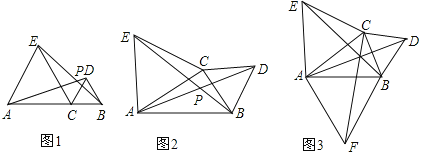
���𰸡���1��AD=BE����2��AD=BE��������APE�����š�ACB�Ĵ�С�����仯��ʼ����60�㣻��3��֤��������
��������
�����������1��ֱ��д���𰸼��ɣ�
��2��֤����ECB�ա�ACD���õ���CEB=��CAD����Ϊ����Ĺؼ��Խ��ۣ������ڽǺͶ������ɽ�����⣮
��3����ͼ���������ߣ�֤����CPA�ա�CHE�����ɽ�����⣮
�����������1���ߡ�ACE����CBD��Ϊ�ȱ������Σ�
��AC=EC��CD=CB����ACE=��BCD��
���ACD=��ECB��
�ڡ�ACD���ECB�У�
 ��
��
���ACD�ա�ECB��SAS����
��AD=BE��

��2��AD=BE��������APE�����š�ACB�Ĵ�С�����仯��ʼ����60�㣮
֤�����ߡ�ACE�͡�BCD�ǵȱ�������
��EC=AC��BC=DC��
��ACE=��BCD=60�㣬
���ACE+��ACB=��BCD+��ACB������ECB=��ACD��
�ڡ�ECB�͡�ACD�У�

���ECB�ա�ACD��SAS����
���CEB=��CAD��
��BE��AC����Q��
�֡ߡ�AQP=��EQC����AQP+��QAP+��APQ=��EQC+��CEQ+��ECQ=180��
���APQ=��ECQ=60�㣬����APE=60�㣮
��3���ɣ�2��ͬ���ɵá�CPE=��EAC=60�㣻��PE�Ͻ�ȡPH=PC������HC��
���PCHΪ�ȱ������Σ�
��HC=PC����CHP=60�㣬
���CHE=120�㣻
�֡ߡ�APE=��CPE=60�㣬
���CPA=120�㣬
���CPA=��CHE��
�ڡ�CPA�͡�CHE�У�
 ��
��
���CPA�ա�CHE��AAS����
��AP=EH��
��PB+PC+PA=PB+PH+EH=BE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD�ij�ABΪ5����BCΪ4��E��BC���ϵ�һ�����㣬AE��EF��EF��CD�ڵ�F����BE=x��FC=y�����E�ӵ�B�˶�����Cʱ���ܱ�ʾy����x�ĺ�����ϵ�Ĵ���ͼ���ǣ� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ཫ��ȫ֪ʶ�����ɼ���������Ƴ�ֱ��ͼ��ͼ�д�������ǰ����İٷֱȷֱ���4%��12%��40%��28%���������Ƶ����8������ �ð���50��ͬѧ�������� ������İٷֱ�Ϊ16%���� �ɼ���70��80�ֵ�������ࣻ�� 80�����ϵ�ѧ����14����������ȷ�ĸ����У� ��
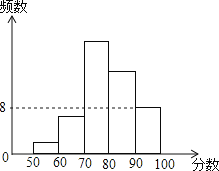
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У�������ǣ�������
A.����ʽx��5�����������������
B.����ʽ��2x��8�Ľ⼯��x����4
C.����ʽx����5�ĸ�������������
D.��40�Dz���ʽ2x����8��һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���װ��ĵľ�����У�ij��45��ͬѧ�����ͳ�����£�
��Ԫ�� | 20 | 30 | 35 | 50 | 100 |
ѧ�������ˣ� | 5 | 10 | 5 | 15 | 10 |
����λ�У��ð�ͬѧ��������������λ���ֱ��ǣ� ��
A.30��35
B.50��35
C.50��50
D.15��50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������a1 �� a2 �� a3��an�ķ���Ϊ2��������2a1+2��2a2+2��2a3+2��2an+2�ķ���Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���kx2+��1��k��x��1=0������˵����ȷ���ǣ� ��
A.��k=0ʱ��������
B.��k=1ʱ��������һ��ʵ����
C.��k=��1ʱ��������������ȵ�ʵ����
D.��k��0ʱ������������������ȵ�ʵ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com