
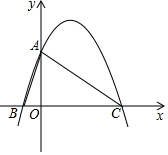 如图,△ABC是直角三角形,∠BAC=90°,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,如图所示建立平面直角坐标系.
如图,△ABC是直角三角形,∠BAC=90°,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,如图所示建立平面直角坐标系.分析 (1)由射影定理可得出B点坐标,进而利用勾股定理得出B,C点坐标,再利用待定系数法求二次函数解析式即可;
(2)过P作x轴的垂线,交AC于Q,交x轴于H;设出点P的横坐标(设为m),根据抛物线和直线AC的解析式,即可表示出P、Q的纵坐标,从而可得到PQ的长,然后分两种情况进行讨论:
①P点在第一象限时,即0<m<8时,可根据PQ的长以及A、C的坐标,分别表示出△APQ、△CPQ的面积,它们的面积和即为△APC的面积,由此可得到S的表达式,通过配方即可得到S的取值范围;
②当P在第二象限时,即-2≤m<0时,同①可求得△APQ、△CPQ的面积,此时它们的面积差为△APC的面积,同理可求得S的取值范围;根据两个S的取值范围,即可判断出所求的结论;
(3)分别利用:①当BQ=QC时,②当BC=CQ1时,③当BQ3=BC时,结合勾股定理求出答案.
解答 解:(1)∵∠BAC=90°,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,
∴BC=10,
∴AO=$\frac{2\sqrt{5}×4\sqrt{5}}{10}$=4,
则BO=2,故CO=8,
即B(-2,0),C(8,0),A(0,4),
设经过点A、B、C的抛物线的解析式为:y=a(x+2)(x-8),
则4=a(0+2)(0-8),
解得:a=-$\frac{1}{4}$,
故y=-$\frac{1}{4}$(x+2)(x-8)=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4,
(2)设直线AC对应的函数解析式为:y=kx+b,
则$\left\{\begin{array}{l}{b=4}\\{8k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
∴直线AC对应的函数解析式为:y=-$\frac{1}{2}$x+4,
如图,过P作PH⊥OC,垂足为H,交直线AC于点Q;
设P(m,-$\frac{1}{4}$m2+$\frac{3}{2}$m+4),则Q(m,-$\frac{1}{2}$m+4).
①当0<m<8时,
PQ=(-$\frac{1}{4}$m2+$\frac{3}{2}$m+4)-(-$\frac{1}{2}$m+4)=-$\frac{1}{4}$m2+2m,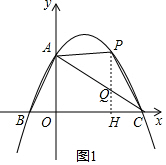
S=S△APQ+S△CPQ=$\frac{1}{2}$×8×(-$\frac{1}{4}$m2+2m)=-(m-4)2+16,
∴0<S≤16;
②当-2≤m<0时,
PQ=(-$\frac{1}{2}$m+4)-(-$\frac{1}{4}$m2+$\frac{3}{2}$m+4)=$\frac{1}{4}$m2-2m,
S=S△CPQ-S△APQ=$\frac{1}{2}$×8×($\frac{1}{4}$m2-2m)=(m-4)2-16,
∴0<S<20;
∴当0<S<16时,0<m<8中有m两个值,-2≤m<0中m有一个值,此时有三个;
当16<S<20时,-2≤m<0中m只有一个值;
当S=16时,m=4或m=4-4$\sqrt{2}$这两个.
故当S=16时,相应的点P有且只有两个;
(3)如图2所示:①当BQ=QC时,∵B(-2,0),C(8,0),
∴Q点横坐标为:3,
则y=-$\frac{1}{2}$×3+4=$\frac{5}{2}$,
故此时Q点坐标为:(3,$\frac{5}{2}$),
②当BC=CQ1时,
设Q1(x,-$\frac{1}{2}$x+4),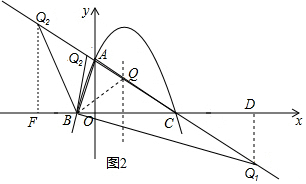
过点Q1D⊥x轴于点D,
则DC=x-8,DQ1=-$\frac{1}{2}$x+4,
故DC2+Q1D2=Q1C2,
期(x-8)2+(-$\frac{1}{2}$x+4)2=100,
解得:x1=8+4$\sqrt{5}$,x2=8-4$\sqrt{5}$,
故y=-2$\sqrt{5}$,或y=2$\sqrt{5}$,
可得Q1(8+4$\sqrt{5}$,-2$\sqrt{5}$),Q2(8-4$\sqrt{5}$,2$\sqrt{5}$);
③当BQ3=BC时,
同理可得:Q3F=-$\frac{1}{2}$x+4,FB=2-x,
故(2-x)2+(-$\frac{1}{2}$x+4)2=100,
解得:x1=8(不合题意舍去),x2=-8,
则y=8,
故Q3(-8,8),
综上所述:使△QBC为等腰三角形的所有符合条件的点Q的坐标分别为:(3,$\frac{5}{2}$),(8+4$\sqrt{5}$,-2$\sqrt{5}$),(8-4$\sqrt{5}$,2$\sqrt{5}$),(-8,8).
点评 此题考查了二次函数图象与坐标轴交点坐标的求法、图形面积的求法、等腰三角形的性质以及勾股定理等知识,正确利用分类讨论分析是解题关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
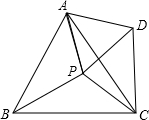 如图,P是等边三角形ABC内一点,∠APB、∠BPC、∠CPA的度数比为4:5:6,以AP为边作正△APD,连接DC,则△PDC的三个内角度数从小到大的比为3:5:9.
如图,P是等边三角形ABC内一点,∠APB、∠BPC、∠CPA的度数比为4:5:6,以AP为边作正△APD,连接DC,则△PDC的三个内角度数从小到大的比为3:5:9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com