
【题目】横卧于清波之上的黄石大桥与已经贯通的五峰山隧道将成为恩施城区跨越东西方向的最大直线通道,它把六角亭老城区与知名景点女儿城连为一体,缓解了恩施城区交通拥堵的现状.如图,某数学兴趣小组利用无人机在五峰山隧道正上空点P处测得黄石大桥西端点A的俯角为30°,东端点B(隧道西进口)的俯角为45°,隧道东出口C的俯角为22°,已知黄石大桥AB全长175米,隧道BC的长约多少米(计算结果精确到1米)?(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() 1.4,
1.4,![]() 1.7)
1.7)
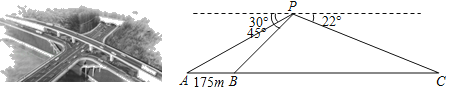
【答案】隧道BC的长约827米.
【解析】
可以作PD⊥AC于点D,根据题意得∠PAD=30°,∠PBD=45°,∠PCD=22°,AB=175,设PD=BD=x,则AD=175+x,根据三角函数求得BD,DC的长即可.
解:如图,作PD⊥AC于点D,
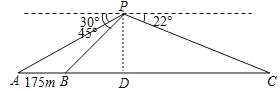
根据题意可知:
∠PAD=30°,∠PBD=45°,∠PCD=22°,AB=175,
设PD=BD=x,则AD=175+x,
在Rt△APD中,tan30°=![]()
即![]() =
=![]() ,
,
解得x=![]() .
.
在Rt△CPD中,tan22°=![]() ,
,
即![]() =0.40,
=0.40,
∴DC=![]() ×
×![]() =
=![]() ,
,
∴BC=BD+DC=![]() =236.25+590.625=826.875≈827(米).
=236.25+590.625=826.875≈827(米).
答:隧道BC的长约827米.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,连接BD,点E在AB上,连接CE交BD于点F,作FG⊥BC于点G,∠BEC=3∠BCE,BF=![]() DF,若FG=
DF,若FG=![]() ,则AB的长为_____.
,则AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一点,且
边上一点,且![]() .点
.点![]() 从点
从点![]() 出发.沿射线
出发.沿射线![]() 以每秒1个单位长度的速度运动.以
以每秒1个单位长度的速度运动.以![]() 、
、![]() 为邻边作
为邻边作![]() .设
.设![]() 和
和![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() (平方单位),点
(平方单位),点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)![]() .
.
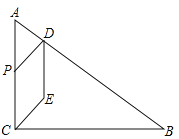
(1)连结![]() ,求
,求![]() 的长.
的长.
(2)当![]() 为菱形时,求
为菱形时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)将线段![]() 沿直线
沿直线![]() 翻折得到线段
翻折得到线段![]() .当点
.当点![]() 落在
落在![]() 的边上时,直接写出
的边上时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,且抛物线上任意不同两点
,且抛物线上任意不同两点![]() 都满足:当
都满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;抛物线与
;抛物线与![]() 轴另一个交点为
轴另一个交点为![]() ,与
,与![]() 轴交于
轴交于![]() 点,对称轴与
点,对称轴与![]() 轴交于
轴交于![]() 点.
点.
(1)求抛物线的对称轴及点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴的平行线交抛物线的对称轴于点
轴的平行线交抛物线的对称轴于点![]() ,当四边形
,当四边形![]() 是正方形时,求抛物线的解析式;
是正方形时,求抛物线的解析式;
(3)在(2)的条件下,垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() 和
和![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
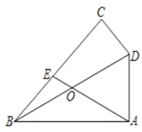
【题目】如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,连接BD,点O为BD的中点,连接AO并延长交BC于点E,若![]() ,CD=4,则AD的长为_____.
,CD=4,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
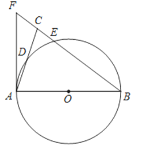
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
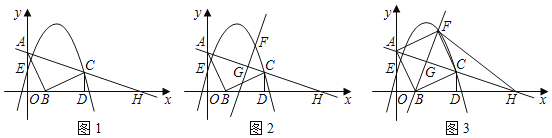
如图1,![]() 的直角顶点
的直角顶点![]() 在坐标原点,点
在坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标及抛物线的表达式;
的坐标及抛物线的表达式;
(2)如图2,已知点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() (点
(点![]() 在第一象限),设点
在第一象限),设点![]() 的横坐标为
的横坐标为![]() .
.
①点![]() 的纵坐标用含
的纵坐标用含![]() 的代数式表示为________;
的代数式表示为________;
②如图3,当直线![]() 经过点
经过点![]() 时,求点
时,求点![]() 的坐标,判断四边形
的坐标,判断四边形![]() 的形状并证明结论;
的形状并证明结论;
③在②的前提下,连接![]() ,点
,点![]() 是坐标平面内的点,若以
是坐标平面内的点,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出点
全等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, ![]() ,
, ![]() 与
与![]() 成正比例,
成正比例, ![]() 与
与![]() 成反比例,并且当
成反比例,并且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() .
.
【解析】分析:(1)首先根据![]() 与x成正比例,
与x成正比例, ![]() 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出![]() 和
和![]() 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
本题解析:
(![]() )设
)设![]() ,
, ![]() ,
,
则![]() ,
,
∵当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴
解得, ![]() ,
,
∴![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(![]() )把
)把![]() 代入
代入![]() 得,
得,
![]() ,
,
解得: ![]() ,
, ![]() .
.
点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24
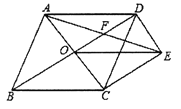
【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com