
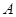 地出发前往
地出发前往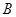 地,且两人到达
地,且两人到达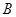 地后各自按原速度返回,且不停地在
地后各自按原速度返回,且不停地在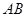 之间往返行驶,甲的速度为32
之间往返行驶,甲的速度为32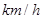 ,乙的速度为18
,乙的速度为18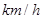 ,当乙车由
,当乙车由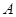 至
至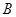 多次后,甲车两次追上乙车,且第二次追上乙时是在乙车从
多次后,甲车两次追上乙车,且第二次追上乙时是在乙车从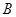 地向
地向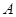 地行驶的途中,且他们此时距
地行驶的途中,且他们此时距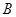 地的距离为10
地的距离为10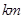 ,则
,则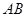 两地相距__________
两地相距__________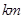 .
.科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
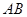 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段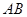 为直径的圆.
为直径的圆.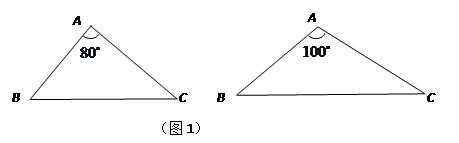
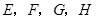 (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.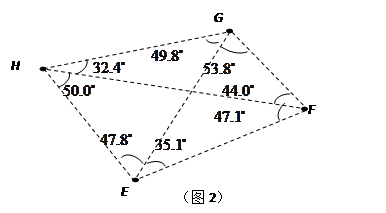
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
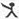 ”、“
”、“ ”定义新运算:对于任意实数a,b,都有a
”定义新运算:对于任意实数a,b,都有a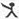 b=a和a
b=a和a b=b,例如3
b=b,例如3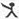 2=3,3
2=3,3 2=2. 则(2011
2=2. 则(2011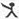 2010)
2010)  (2009
(2009 2008)=_______________.
2008)=_______________.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com