练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如图，在水池的正中央有一根芦苇，池底长10尺，它高出水而1尺，如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面则这根芦苇的长度是（　　）
    A．10尺B．11尺C．12尺D．13尺

    分析 找到题中的直角三角形，设水深为x尺，根据勾股定理解答．

    解答 解：设水深为x尺，则芦苇长为（x+1）尺，
    根据勾股定理得：x2+（$\frac{10}{2}$）2=（x+1）2，
    解得：x=12，
    芦苇的长度=x+1=12+1=13（尺），
    故选D．

    点评 本题考查正确运用勾股定理．善于观察题目的信息是解题以及学好数学的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．按一定规律排列的一组数据：-$\frac{1}{2}$，$\frac{4}{3}$，-$\frac{9}{4}$，$\frac{16}{5}$，-$\frac{25}{6}$…，则第n个数据可表示为（-1）n$\frac{{n}^{2}}{n+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．由$\frac{1}{1×2}$=$\frac{1}{2}$=1-$\frac{1}{2}$；
    $\frac{1}{2×3}$=$\frac{1}{6}$=$\frac{1}{2}$-$\frac{1}{3}$；
    $\frac{1}{3×4}$=$\frac{1}{12}$=$\frac{1}{3}$-$\frac{1}{4}$，
    …
    你能总结出$\frac{1}{n（n+1）}$=？（n为正整数）
    并试着化简：
    （1）$\frac{1}{x（x+1）}$+$\frac{1}{（x+1）（x+2）}$+$\frac{1}{（x+2）（x+3）}$+…+$\frac{1}{（x+8）（x+9）}$；
    （2）$\frac{1}{（x-2）（x-3）}$-$\frac{2}{（x-1）（x-3）}$+$\frac{1}{（x-1）（x-2）}$；
    （3）解方程$\frac{1}{{x}^{2}-5x+6}$-$\frac{1}{{x}^{2}-4x+3}$+$\frac{1}{{x}^{2}-3x+2}$=$\frac{1}{x-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．在学习了“多边形的内角和”后，小明和小艳有一段对话，如下：
    小明：这个多边形的内角和是2750°．
    小艳：不对呀！仔细检查下，看你少加了一个内角．
    请你解答下列问题：
    （1）小明是在求几边形的内角和？
    （2）少加的那个内角为多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

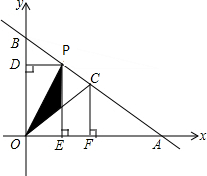    15．如图，点A，B坐标分别为（8，0）、（0，6），点C是线段AB的中点，点P是射线BA上一动点，过P作PD⊥y轴于D，PE⊥x轴于E，设OE=t，矩形OEPD与△POC重合部分的面积为S．
    （1）求线段OC所在直线的解析式；
    （2）求S与t的函数关系式；
    （3）当点P在线段AB上时，求S的最大值；
    （4）若S=2，则t的值有4个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

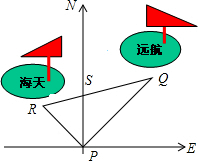    5．如图，某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口，各自沿同定方向航行，“远航”号每小时航行16n mile，“海天”号每小时航行12n mile，它们离开港口一个半小时后分别位于点Q，R处，且相距30n mile
    （1）求PQ，PR的长度；
    （2）如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：（-3）2+$\sqrt{4}$-（π-3.14）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．在无锡全民健身越野赛中，甲、乙两选手的行程y（千米）随时间（时）变化的图象（全程）如图所示．下列四种说法：
    ①起跑后1小时内，甲在乙的前面；   ②第1小时两人都跑了10千米；
    ③甲比乙先到达终点；               ④两人都跑了20千米．
    正确的有（　　）
    A．①②③④B．①②③C．①②④D．②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

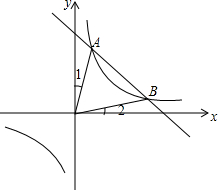    9．如图，函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A，B两点，已知A点的坐标为（1，4）．
    （1）当k1的值；
    （2）当x＜1时，观察图象，比较y1与y2的大小；
    （3）分别连接OA，OB，当∠1=∠2时，求y2关于x的函数表达式．

    查看答案和解析>>

    同步练习册答案