
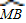 上任取一点E(点E与点B不重合),EB的延长线交优弧
上任取一点E(点E与点B不重合),EB的延长线交优弧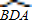 于点F,如图所示,连接AE、AF,则AE______AB(请在横线上填上“≥、≤、<、>”这四个不等号中的一个)并加以证明.(友情提示:结论要填在答题卡相应的位置上)
于点F,如图所示,连接AE、AF,则AE______AB(请在横线上填上“≥、≤、<、>”这四个不等号中的一个)并加以证明.(友情提示:结论要填在答题卡相应的位置上)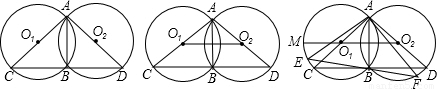
 CD=CB,所以四边形O1CBO2是平行四边形;
CD=CB,所以四边形O1CBO2是平行四边形;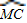 上(不与点C重合)时,当点E在劣弧
上(不与点C重合)时,当点E在劣弧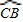 上(不与点B重合)时,证得AE>AB.
上(不与点B重合)时,证得AE>AB. CD=CB.(6分)
CD=CB.(6分)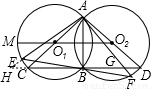 ②解:AE>AB,(8分)
②解:AE>AB,(8分)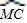 上(不与点C重合)时,
上(不与点C重合)时,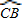 上(不与点B重合)时,设AE交CD与H,
上(不与点B重合)时,设AE交CD与H,

科目:初中数学 来源: 题型:
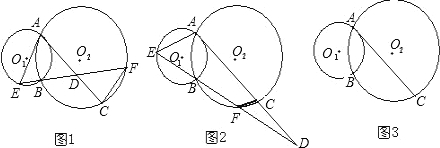
 11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.
11、如图,已知:⊙O1与⊙O2是等圆,它们相交于A、B两点,O2在⊙O1上,AC是⊙O2的直径,直线CB交⊙O1于D,E为AB延长线上一点,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com