
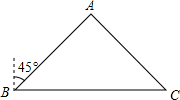
 某物流公司派送人员甲、乙分别从B地派送货物到A、C两地,如图,A在B的北偏东45°方向,C在B的正东方向且BC=120km.乙的速度是60km/h,甲的速度是乙速度的$\sqrt{2}$倍,甲把货物送到A地后又接到A地一批货物要送到C地,结果两人同时到达C地.
某物流公司派送人员甲、乙分别从B地派送货物到A、C两地,如图,A在B的北偏东45°方向,C在B的正东方向且BC=120km.乙的速度是60km/h,甲的速度是乙速度的$\sqrt{2}$倍,甲把货物送到A地后又接到A地一批货物要送到C地,结果两人同时到达C地.分析 (1)作AD⊥BC于D,由题意求出∠ABC=45°,△ABD是等腰直角三角形,得出AB=$\sqrt{2}$BD,由甲的速度是乙速度的$\sqrt{2}$倍,得出△ACD是等腰直角三角形,∠DAC=45°,求出∠BAC=90即可;
(2)由(1)得出△ABC是等腰直角三角形,AD=BD=CD,由乙的速度求出乙到C地的时间,得出当0<t≤1时,s=60t;当1<t≤2时,s=120-60t;即可得出结论.
解答 解:(1)作AD⊥BC于D,如图所示: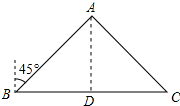
由题意得:∠ABC=90°-45°=45°,
∴△ABD是等腰直角三角形,
∴AB=$\sqrt{2}$BD,
∵甲的速度是乙速度的$\sqrt{2}$倍,
∴AC=$\sqrt{2}$CD,
∴△ACD是等腰直角三角形,
∴∠DAC=45°,
∴∠BAC=45°+45°=90°;
故答案为:90;
(2)由(1)得:△ABC是等腰直角三角形,AD=BD=CD,
∵乙的速度是60km/h,BC=120km,
∴120÷60=2(h),
∴当0<t≤1时,s=60t;
当1<t≤2时,s=120-60t;
当t=1时,s=AD=$\frac{1}{2}$BC=60,
即当t为何值时,两人间的距离最大,最大值是60km.
点评 本题考查了解直角三角形的运用-方向角问题、等腰直角三角形的判定与性质;证出∠BAC=90°是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 消费金额(元) | 300 | 200 | 400 | 500 | 400 | 300 | 600 | 300 | 400 | 800 | 300 | 300 |
| A. | 400,300 | B. | 300,400 | C. | 400,400 | D. | 300,300 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
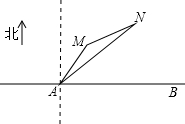 如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.
光伏发电惠民生,据衢州晚报载,某家庭投资4万元资金建造屋顶光伏发电站,遇到晴天平均每天可发电30度,其它天气平均每天可发电5度,已知某月(按30天计)共发电550度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com