
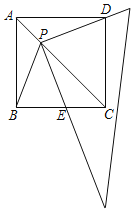
【题目】如图,一直角三角形的直角顶点P在边长为1的正方形ABCD对角线AC上运动(点P与A、C两点不重合)且它的一条直角边始终经过点D,另一直角边与射线BC交于点E.
(1)当点E在BC边上时,
①求证:△PBC≌△PDC;
②判断△PBE的形状,并说明理由;
(2)设AP=x,△PBE的面积为y.
①求出y关于x的函数关系式,并写出x的取值范围;
②当x取何值时,y取得最大值,并求出这个最大值.
【答案】(1)①见解析;②△PBE是等腰三角形;(2)①![]() ;当x=
;当x=![]() 时,y最大值=
时,y最大值=![]() .
.
【解析】
(1)①根据SAS证明两三角形全等;
②由△PBC≌△PDC得∠PBC=∠PDC,由∠BCD=∠DPE=90°,∠PEB=∠PDC,∠PEB=∠PBC即可证明PB=PE,即△PBE为等腰三角形;
(2)①作高线PF,分别计算BE和PF的长,根据三角形面积公式可得y关于x的函数关系式;
②将①中所得二次函数的解析式配方后可得结论.
解:(1)①∵四边形ABCD是正方形,
∴BC=DC,∠BCD=90°,AC平分∠BCD.
∴∠BCP=∠DCP=45°.
∵PC=PC,
∴△PBC≌△PDC (SAS);
②△PBE是等腰三角形,理由是:
由△PBC≌△PDC可知,∠PBC=∠PDC.
∵∠BCD=∠DPE=90°,
∴∠PDC+∠PEC=180°,
又∠PEB+∠PEC=180°,
∴∠PEB=∠PDC,
∴∠PEB=∠PBC.
∴PB=PE,即△PBE是等腰三角形.
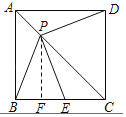
(2)①如图1,过点P作PF⊥BC,垂足为F,则BF=FE.
∵AP=x,AC=![]() ,
,
∴PC=![]() ﹣x,PF=FC=
﹣x,PF=FC=![]()
BF=FE=1﹣FC=1﹣(1﹣![]() x)=
x)=![]() x.
x.
∴S△PBE=![]() =BFPF=
=BFPF=![]() x(1﹣
x(1﹣![]() x)=
x)=![]() .
.
即 ![]()
②y=![]() =
=![]()
∵a=﹣![]() <0,
<0,
∴当x=![]() 时,y最大值=
时,y最大值=![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
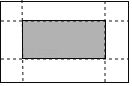
A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() ,
,![]() ,
,![]() 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称![]() ,
,![]() ,
,![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() ,
,![]() ,
,![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店新进一种台灯.这种台灯的成本价为每个30元,经调查发现,这种台灯每天的销售量y(单位:个)是销售单价x(单位:元)(30≤x≤60)的一次函数.
x | 30 | 35 | 40 | 45 | 50 |
y | 30 | 25 | 20 | 15 | 10 |
(1)求销售量y与销售单价x之间的函数表达式;
(2)设这种台灯每天的销售利润为w元.这种台灯销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校课程中心为了了解学生对开设的3D打印、木工制作、机器人和电脑编程四门课程的喜爱程度,随机调查了部分学生,每人只能选一项最喜爱的课程.图①是四门课程最喜爱人数的扇形统计图,图②是四门课程男、女生最喜爱人数的条形统计图.
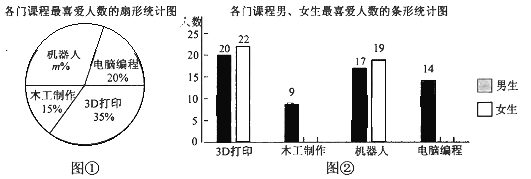
(1)求图①中![]() 的值,补全图②中的条形统计图,标上相应的人数;
的值,补全图②中的条形统计图,标上相应的人数;
(2)若该校共有1800名学生,则该校最喜爱3D打印课程的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c②9a+3b+c>0:③b2<4ac④c=﹣3a⑤当y<0时,﹣1<x<3,其中正确的个数是_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红参加学校组织的庆祝党的十九大胜利召开知识竞赛,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,可是小红这两道题都不会,不过竞赛规则规定每位选手有两次求助机会,使用“求助”一次可以让主持人去掉其中一题的一个错误选项,主持人提醒小红可以使用两次“求助”.
(1)如果小红两次“求助”都在第一道题中使用,那么小红通关的概率是 .
(2)如果小红将每道题各用一次“求助”,请用树状图或者列表来分析她顺序通关的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com