
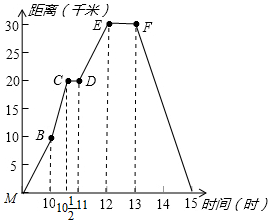
 如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:
如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:分析 (1)根据函数图象,可以得到小丽什么时间离家最远,离家最远距离是多少;
(2)根据函数图象可以解答本题;
(3)根据函数图象可以得到小丽离家的距离是15千米有两个时刻,然后分别计算出相应的时刻即可.
解答 解:(1)由图象可得,
小丽在12点-13点离家最远,离家最远距离是30千米;
(2)由图象可得,
小丽一共休息了两次,第一次是从10:30开始,休息30分钟,第二次是从12点开始,休息了1个小时;
(3)由图象可得,
小丽离家15千米一个是在BC段,一个在F到回到家中这个阶段,
当在BC段时,10+(15-10)÷[(20-10)×(10.5-10)]=10.5,
即第一次距家15千米是在10:30;
第二次是:13+(30-15)÷[30÷(15-13)]=14,
即第二次距家15千米是在14:00.
点评 本题考查函数图象,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
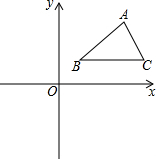 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(8,6),B(3,2),C(9,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
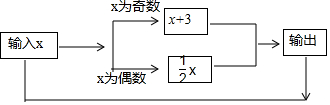
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com