
【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

【答案】(1)相等;(2)相等.
【解析】试题分析:
(1)甲所走的路径长为以AB为直径的半圆长,乙所走的路径长为以AC和BC为直径的两个半圆长的和,然后根据圆的周长公式进行计算,再比较大小即可;
(2)甲所走的路径长为以AB为直径的半圆长,乙所走的路径长为以AC、CD和DB为直径的三个半圆长的和,然后根据圆的周长公式分别计算他们所走的路径,再比较大小即可.
试题解析:
(1)BC=AB-AC=10,
甲所走的路径长=![]() 2π
2π![]() =
=![]() 2π
2π![]() =20π(m),
=20π(m),
乙所走的路径长=![]() 2π
2π![]() +
+![]() 2π
2π![]() =
=![]() 2π
2π![]() +
+![]() π
π![]() =20π(m),
=20π(m),
所以两人所走路程的相等;
(2)两人走的路程远近相同.理由如下:甲所走的路径长=![]() 2π
2π![]() =
=![]() πAB,
πAB,
乙所走的路径长=![]() 2π
2π![]() +
+![]() 2π
2π![]() +
+![]() π
π![]() =
=![]() π(AC+CD+DB)=
π(AC+CD+DB)=![]() πAB,
πAB,
即两人走的路程远近相同.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.
与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3为边长作等边△A3A2B3,…,则等边△A2017A2018B2018的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
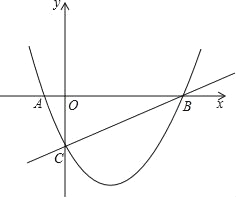
【题目】如图,已知抛物线y=ax2﹣![]() x+c与x轴相交于A、B两点,并与直线y=
x+c与x轴相交于A、B两点,并与直线y=![]() x﹣2交于B、C两点,其中点C是直线y=
x﹣2交于B、C两点,其中点C是直线y=![]() x﹣2与y轴的交点,连接AC.
x﹣2与y轴的交点,连接AC.
(1)求抛物线的解析式;
(2)证明:△ABC为直角三角形;
(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=﹣6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”
译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?鸡的价钱是多少?”设有x个人共同买鸡,根据题意列一元一次方程,正确的是( )

A. 9x+11=6x﹣16B. 9x﹣11=6x+16
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:
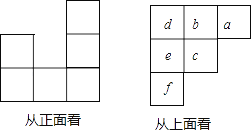
(1)a,b,c各表示几?
(2)这个几何体最少有几个小立方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体从左面看到的形状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB与点O,若BC=8,AO=3,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,线段AB上有两个点C、D,请计算图中共有多少条线段?
![]()
(2)如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?
(3)拓展应用:8个班级参加学校组织的篮球比赛,比赛采用单循环制(即每两个班级之间都要进行一场比赛),那么一共要进行多少场比赛?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com