⊙O的半径为5cm,弦AB∥CD,AB=6cm,CD=8cm,则AB和CD的距离是( )
A.7cm
B.8cm
C.7cm或1cm
D.1cm
【答案】
分析:因为AB、CD位置不明确,所以分在圆心的同一侧和圆心两侧两种情况讨论.
解答:解:本题要分类讨论:
(1)AB,CD在圆心的同侧,如图①,连接OA、OC,过O作AB的垂线交CD,AB于E、F,
根据垂径定理得ED=

CD=

×8=4cm,FB=

AB=

×6=3cm,
在Rt△OED中,OD=5cm,ED=4cm,由勾股定理得OE=
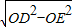
=
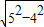
=3cm,
在Rt△OFB中,OB=5cm,FB=3cm,则OF=
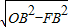
=
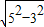
=4cm,
AB和CD的距离=OF-OE=4-3=1cm;
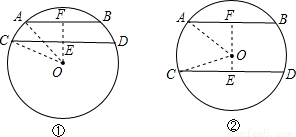
(2)AB,CD在圆心的异侧,如图②,连接OA、OC,过O作AB的垂线交CD,AB于E、F,
根据垂径定理得ED=

CD=

×8=4cm,FB=

AB=

×6=3cm,
在Rt△OED中,OD=5cm,ED=4cm,由勾股定理得OE=
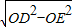
=
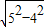
=3cm,
在Rt△OFB中,OB=5cm,FB=3cm,则OF=
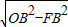
=

=4cm,
AB和CD的距离是OF+OE=4+3=7cm.
AB和CD的距离是7cm或1cm.
故选C.
点评:本题涉及到垂径定理及勾股定理,解题时要注意分类讨论,不要漏解.

 CD=
CD= ×8=4cm,FB=
×8=4cm,FB= AB=
AB= ×6=3cm,
×6=3cm,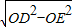 =
=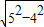 =3cm,
=3cm,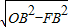 =
=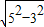 =4cm,
=4cm,
 CD=
CD= ×8=4cm,FB=
×8=4cm,FB= AB=
AB= ×6=3cm,
×6=3cm,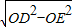 =
=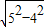 =3cm,
=3cm,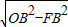 =
= =4cm,
=4cm,
