
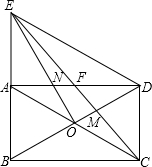
 如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.
如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.分析 (1)先判定△BDE是等边三角形,再根据等边三角形的性质得出AB=AE,最后根据AE=CD,AE∥CD,得出四边形EACD是平行四边形;
(2)根据平行四边形ACDE中DE∥CO,判定△COM∽△EDM,再根据相似三角形的性质得出$\frac{OM}{DM}$=$\frac{CO}{ED}$,进而求得$\frac{OM}{MD}$的值;
(3)先根据等边三角形的轴对称性质得出,△NOB与△NOD、△NAB、△NAE的面积均相等,再根据MN∥DE以及CO∥DE,运用同底等高的三角形面积相等,分别得出△EOM、△DCM与△NOB面积相等即可.
解答 解:(1)∵矩形ABCD中,BO=DO,EO⊥BD,
∴EO垂直平分BD,
∴EB=ED,
又∵∠ABD=60°,
∴△BDE是等边三角形,
又∵DA⊥BE,
∴AB=AE,
∵矩形ABCD中,CD∥BA,CD=AB,
∴AE=CD,AE∥CD,
∴四边形EACD是平行四边形;
(2)∵四边形EACD是平行四边形,
∴DE=AC,DE∥CO,
∴△COM∽△EDM,
∴$\frac{OM}{DM}$=$\frac{CO}{ED}$,
又∵CO=$\frac{1}{2}$AC,DE=AC,
∴CO=$\frac{1}{2}$DE,
∴$\frac{OM}{MD}$=$\frac{1}{2}$;
(3)连接BN,则
由等边△BDE的轴对称性可得,△NOB与△NOD、△NAB、△NAE的面积均相等,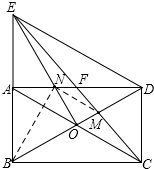
由(2)可得,$\frac{OM}{MD}$=$\frac{1}{2}$,
同理可得,$\frac{ON}{NE}=\frac{1}{2}$,
∴$\frac{OM}{OD}=\frac{ON}{OE}=\frac{1}{3}$,
∴MN∥DE,
∴△MNE与△MND的面积相等,
∴△FNE与△FMD的面积相等,
∴△EOM与△DON的面积相等,
由CO∥DE可得,△OCE与△COD的面积相等,
∴△EOM与△DCM的面积相等,
综上,与△NOB面积相等的三角形有:△NOD、△NAB、△NAE、△EOM、△DCM这5个.
故答案为:5
点评 本题主要考查了四边形的综合应用,解决问题的关键是掌握等边三角形的判定与平行四边形的判定方法.在解题时注意:如果一条直线截三角形的两边所得的对应线段成比例,那么这条直线平行于三角形的第三边,据此可以得到同底等高的三角形面积相等.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
 如图,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值为( )
如图,要拧开一个边长是2的正六边形螺母,扳手张开的开口a的取值为( )| A. | 2$\sqrt{3}$≤a≤4 | B. | a≤4 | C. | $\sqrt{3}$≤a≤2 | D. | a≥2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 阅读时间t/h | 0≤t<2 | 2≤t<4 | 4≤t<6 | 6≤t<8 |
| 频数 | 5 | 11 | 4 |
| A. | 12.5% | B. | 40% | C. | 50% | D. | 60% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某市中学生立定跳远的情况 | |
| B. | 调查某市市民对央视春晚的喜爱程度 | |
| C. | 调查某市市民的晨练情况 | |
| D. | 调查某班学生校服的尺寸 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连结DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连结DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com