
【题目】如图,将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形.

(1)若用不同的方法计算这个边长为(a+b+c)的正方形面积,就可以得到一个的等式,这个等式可以为 ;
(2)请利用(1)中的等式解答下列问题:
①若三个实数a,b,c满足a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
②若三个实数x,y,z满足2x×4y÷8z=32,x2+4y2+9z2=45,求2xy﹣3xz﹣6yz的值.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)45;(3)-10.
【解析】
(1)根据图形得出等式即可;
(2)①先根据公式进行变形,再代入求出即可;
②先求出x+2y-3z=5,再根据(x+2y-3z)2=x2+4y2+9z2+2(2xy-3xz-6yz)求出即可.
解:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)①∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2
=(a+b+c)2-(2ab+2ac+2bc)
=112-2×38
=45;
②∵2x×4y÷8z=32,
∴2x×22y÷23z=32,
∴2x+2y-3z=25,
∴x+2y-3z=5,
∵(x+2y-3z)2=x2+4y2+9z2+2(2xy-3xz-6yz),
∴x2+4y2+9z2=-10,


科目:初中数学 来源: 题型:
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()

A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
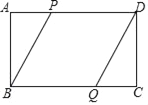
【题目】如图,矩形ABCD中,点P是线段AD上任意一点,点Q为BC上一点,且AP=CQ.
(1)求证:BP=DQ;
(2)若AB=4,且当PD=5时四边形PBQD为菱形.求AD为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
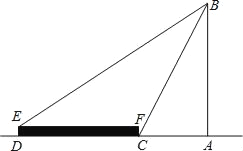
【题目】如图,在一个平台远处有一座古塔,小明在平台底部的点C处测得古塔顶部B的仰角为60°,在平台上的点E处测得古塔顶部的仰角为30°.已知平台的纵截面为矩形DCFE,DE=2米,DC=20米,求古塔AB的高(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农历五月初五是我国传统佳节“端午节”民间历来有吃“粽子”的习俗,某区食品厂为了解市民对去年销售量较好的栗子粽、豆沙粽、红枣粽、蛋黄棕、大肉棕(以下分别用A,B,C,D,E表示)这五种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅不完整统计图.

根据以上统计图解答问题:
(1)本次被调查的市民有 人,请补全条形统计图;
(2)扇形统计图中大肉粽对应的圆心角是 度;
(3)若该区有居民约40万人,估计其中喜爱大肉粽的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
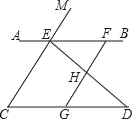
【题目】如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=70°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
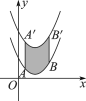
【题目】如图,将函数y=![]() (x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
(x-2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A′,B′,若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(m+1)x2+2mx+(m﹣3)=0有实数根.
(1)求m的取值范围;
(2)m为何值时,方程有两个相等的实数根?并求出这两个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从王同学和李同学中挑选一人参加县知识竞赛在五次选拔测试中他俩的成绩如下表.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
王同学 | 60 | 75 | 100 | 90 | 75 |
李同学 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
王同学 | 80 | 75 | 75 | _____ |
李同学 |
|
|
|
|
(2)在这五次测试中,成绩比较稳定的同学是谁若将80分以上(含80分)的成绩视为优秀,则王同学、李同学在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com