
【题目】如图所示,直线AB与双曲线y=![]() 交于A,B两点,直线AB与x、y坐标轴分别交于C,D两点,连接OA,若OA=2
交于A,B两点,直线AB与x、y坐标轴分别交于C,D两点,连接OA,若OA=2![]() ,tan∠AOC=
,tan∠AOC=![]() ,B(﹣3,m)
,B(﹣3,m)
(1)分别求一次函数与反比例函数式.
(2)连接OB,在x轴上求点P的坐标,使△AOP的面积等于△AOB的面积.
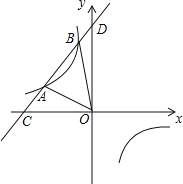
【答案】(1)y=﹣![]() ,y=
,y=![]() x+12;(2)P(9,0)或(﹣9,0)
x+12;(2)P(9,0)或(﹣9,0)
【解析】
(1)过A作AE⊥OC与E,根据已知条件和勾股定理得到A(﹣6,4),由直线AB与双曲线y=![]() 交于A,B两点,得到k=﹣6×4=﹣3m,解方程和方程组即可得到结论;
交于A,B两点,得到k=﹣6×4=﹣3m,解方程和方程组即可得到结论;
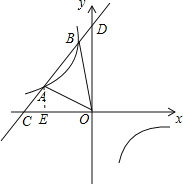
(2)设P(n,0),根据△AOP的面积等于△AOB的面积,列方程即可得到结论.
解:(1)过A作AE⊥OC与E,
∵tan∠AOC=![]() ,
,
∴设AE=2x,OE=3x,
∴AO=![]() =
=![]() x=2
x=2![]() ,
,
∴x=2,
∴AE=4,OE=6,
∴A(﹣6,4),
∴线AB与双曲线y=![]() 交于A,B两点,
交于A,B两点,
∴k=﹣6×4=﹣3m,
∴k=﹣24,m=8,
∴反比例函数式为y=﹣![]() ,B(﹣3,8),
,B(﹣3,8),
设一次函数的解析式为y=kx+b,
∴![]() ,解得:
,解得: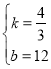 ,
,
∴一次函数的解析式为y=![]() x+12;
x+12;
(2)设P(n,0),
∵△AOP的面积等于△AOB的面积,
∴![]() |n|×4=
|n|×4=![]() (4+8)×3,
(4+8)×3,
∴n=±9,
∴P(9,0)或(﹣9,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数![]() (x>0)的图像经过点D,则
(x>0)的图像经过点D,则![]() 值为( )
值为( )
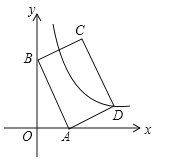
A. ﹣14 B. 14 C. 7 D. ﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…,依次规律,第6个图形有( )个小圆.

A.34B.40C.46D.60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)直接写出抛物线![]() 的解析式;
的解析式;
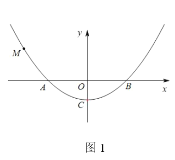
(2)如图1,点![]() 在
在![]() 轴左侧的抛物线
轴左侧的抛物线![]() 上,将点
上,将点![]() 先向右平移4个单位长度,再向下平移
先向右平移4个单位长度,再向下平移![]() 个单位长度,得到的对应点
个单位长度,得到的对应点![]() 恰好落在抛物线
恰好落在抛物线![]() 上,若
上,若![]() ,求点
,求点![]() 的坐标;
的坐标;
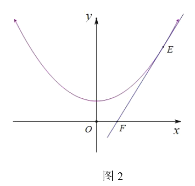
(3)如图2,将抛物线![]() 向上平移2个单位长度得到抛物线
向上平移2个单位长度得到抛物线![]() ,一次函数
,一次函数![]() 的图象
的图象![]() 与抛物线
与抛物线![]() 只有一个公共点
只有一个公共点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,探究:
,探究:![]() 轴上是否存在定点
轴上是否存在定点![]() 满足
满足![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;否则,说明理由.
的坐标;否则,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
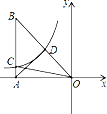
【题目】如图,已知反比函数![]() 的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为
的图象过Rt△ABO斜边OB的中点D,与直角边AB相交于C,连结AD、OC,若△ABO的周长为![]() ,AD=2,则△ACO的面积为( )
,AD=2,则△ACO的面积为( )
A. ![]() B. 1 C. 2 D. 4
B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”“一般”“较强”“很强”四个层次,并绘制成如下两幅尚不完整的统计图
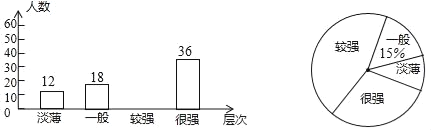
根据以上信息,解答下列问题:
(1)该校有1200名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有多少名?
(2)请直接将条形统计图补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com