
【题目】阅读材料,回答问题:
材料
题1:经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性的大小相同,求三辆汽车经过这个十字路口时,至少要两辆车向左转的概率
题2:有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁(一把钥匙只能开一把锁),第三把钥匙不能打开这两把锁.随机取出一把钥匙开任意一把锁,一次打开锁的概率是多少?
我们可以用“袋中摸球”的试验来模拟题1:在口袋中放三个不同颜色的小球,红球表示直行,绿球表示向左转,黑球表示向右转,三辆汽车经过路口,相当于从三个这样的口袋中各随机摸出一球.
问题:
(1)事件“至少有两辆车向左转”相当于“袋中摸球”的试验中的什么事件?
(2)设计一个“袋中摸球”的试验模拟题2,请简要说明你的方案
(3)请直接写出题2的结果.
【答案】题1.![]() ;题2.(1)至少摸出两个绿球;(2)方案详见解析;(3)
;题2.(1)至少摸出两个绿球;(2)方案详见解析;(3)![]() .
.
【解析】
试题分析:题1:因为此题需要三步完成,所以画出树状图求解即可,注意要做到不重不漏;
题2:根据题意列出表格,得出所有等可能的情况数,找出随机取出一把钥匙开任意一把锁,一次打开锁的情况数,即可求出所求的概率;
问题:
(1)绿球代表左转,所以为:至少摸出两个绿球;
(2)写出方案;
(3)直接写结果即可.
试题解析:题1:画树状图得:
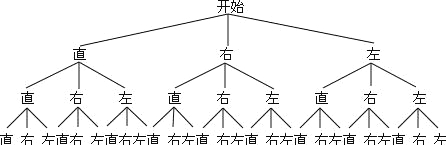
∴一共有27种等可能的情况;
至少有两辆车向左转的有7种:直左左,右左左,左直左,左右左,左左直,左左右,左左左,
则至少有两辆车向左转的概率为:![]() .
.
题2:列表得:
锁1 | 锁2 | |
钥匙1 | (锁1,钥匙1) | (锁2,钥匙1) |
钥匙2 | (锁1,钥匙2) | (锁2,钥匙2) |
钥匙3 | (锁1,钥匙3) | (锁2,钥匙3) |
所有等可能的情况有6种,其中随机取出一把钥匙开任意一把锁,一次打开锁的2种,
则P=![]() =
=![]() .
.
问题:
(1)至少摸出两个绿球;
(2)一口袋中放红色和黑色的小球各一个,分别表示不同的锁;另一口袋中放红色、黑色和绿色的小球各一个,分别表示不同的钥匙;其中同颜色的球表示一套锁和钥匙.“随机取出一把钥匙开任意一把锁,一次打开锁的概率”,相当于,“从两个口袋中各随机摸出一个球,两球颜色一样的概率”;
(3)![]() .
.


科目:初中数学 来源: 题型:
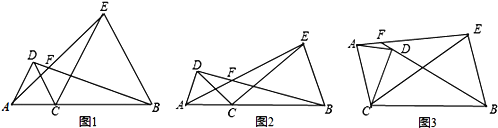
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F
(1)如图1,若∠ACD=60゜,则∠AFB= ;
(2)如图2,若∠ACD=α,则∠AFB= (用含α的式子表示);
(3)将图2中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图3.试探究∠AFB与α的数量关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() +mx﹣2m﹣2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,
+mx﹣2m﹣2与x轴交于A、B两点,点A在点B的左边,与y轴交于点C,
(1)当m=1时,求点A和点B的坐标;
(2)抛物线上有一点D(﹣1,n),若△ACD的面积为5,求m的值;
(3)P为抛物线上A、B之间一点(不包括A、B),PM⊥x轴于点M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用运算律进行简便计算:
(1)(﹣32)÷(﹣2 ![]() )﹣(﹣2)3×
)﹣(﹣2)3× ![]() ﹣5×
﹣5× ![]() ÷4
÷4
(2)3 ![]() +(﹣2
+(﹣2 ![]() )+5
)+5 ![]() +(﹣8
+(﹣8 ![]() )
)
(3)(﹣ ![]() )×(﹣15)×(﹣
)×(﹣15)×(﹣ ![]() )×
)× ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形的上底为a2+2a﹣10,下底为3a2﹣5a﹣80,高为40.(π取3) 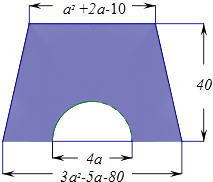
(1)用式子表示图中阴影部分的面积;
(2)当a=10时,求阴影部分面积的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013湖北咸宁)跳远运动员李刚对训练效果进行测试,6次跳远的成绩(单位:m)如下:7.6,7.8,7.7,7.8,8.0,7.9.这六次成绩的平均数为7.8,方差为![]() .如果李刚再跳两次,成绩分别为7.7,7.9,则李刚这8次跳远成绩的方差________.(填“变大”“不变”或“变小”)
.如果李刚再跳两次,成绩分别为7.7,7.9,则李刚这8次跳远成绩的方差________.(填“变大”“不变”或“变小”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com