
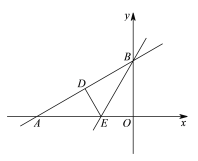
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
与x轴交于点A,与y轴交于点B.将△AOB沿过点B的直线折叠,使点O落在AB边上的点D处,折痕交x轴于点E.
(1)求直线BE的解析式;
(2)求点D的坐标;
【答案】(1)直线BE的解析式为y=![]() x+2
x+2![]() ;(2)D(-3,
;(2)D(-3,![]() ).
).
【解析】
(1)先求出点A、B的坐标,继而根据勾股定理求出AB的长,根据折叠可得BD=BO,DE=OE,从而可得AD的长,设DE=OE=m,则AE=OA-m,在直角三角形AED中利用勾股定理求出m,从而得点E坐标,继而利用待定系数法进行求解即可;
(2)过点D作DM⊥AO,垂足为M,根据三角形的面积可求得DM的长,继而可求得点D的坐标.
(1)![]() ,令x=0,则y=2
,令x=0,则y=2![]() ,
,
令y=0,则![]() ,解得:x=-6,
,解得:x=-6,
∴A(-6,0),B(0,2![]() ),
),
∴OA=6,OB=2![]() ,
,
∴AB=![]() =4
=4![]() ,
,
∵折叠,
∴∠BDE=∠BOA=90°,DE=EO,BD=BO=2![]() ,
,
∴∠ADE=90°,AD=AB-BD=2![]() ,
,
设DE=EO=m,则AE=AO-OE=6-m,
在Rt△ADE中,AE2=AD2+DE2,
即(6-m)2=m2+(2![]() )2,
)2,
解得:m=2,
∴OE=2,
∴E(-2,0),
设直线BE的解析式为:y=kx+b,
把B、E坐标分别代入得: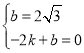 ,
,
解得: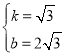 ,
,
∴直线BE的解析式为y=![]() x+2
x+2![]() ;
;
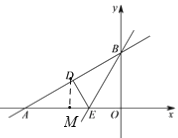
(2)过点D作DM⊥AO,垂足为M,
由(1)DE=2,AE=AO-OE=4,
∵S△ADE=![]() ,
,
即![]() ,
,
∴DM=![]() ,
,
∴点D的纵坐标为![]() ,
,
把y=![]() 代入
代入![]() ,得
,得
![]() ,
,
解得:x=-3,
∴D(-3,![]() ).
).


科目:初中数学 来源: 题型:
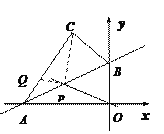
【题目】如图,已知直线![]() 与x轴、y轴分别交于A, B两点,将△AOB沿直线AB翻折,使点O落在点C处, 点P,Q分别在AB , AC上,当PC+PQ取最小值时,直线OP的解析式为( )
与x轴、y轴分别交于A, B两点,将△AOB沿直线AB翻折,使点O落在点C处, 点P,Q分别在AB , AC上,当PC+PQ取最小值时,直线OP的解析式为( )
A. y=- ![]() B. y=-
B. y=- ![]() C. y=-
C. y=- ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断

A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
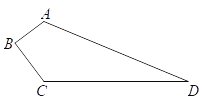
【题目】某小区有一块四边形空地ABCD,如图所示,现计划在这块地上种植每平方米60元的草坪用以美化环境,施工人员测得(单位:米):AB=3,BC=4,CD=12,DA=13,∠B=90°,求小区种植这种草坪需多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求两位数的平方时,可以用“列竖式”的方法进行速算,求解过程如图1所示.
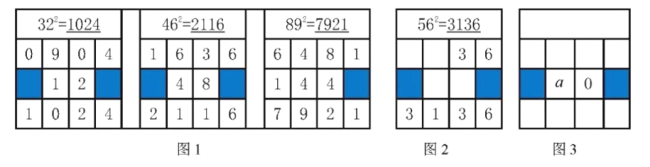
(1)仿照图1,在图2中补全![]() 的“竖式”;
的“竖式”;
(2)仿照图1,用“列竖式”的方法计算一个十位数字是![]() 的两位数的平方,过程部分如图3所示,则这个两位数为 (用含
的两位数的平方,过程部分如图3所示,则这个两位数为 (用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庄子说:“一尺之椎,日取其半,万世不竭”.这句话(文字语言)表达了古人将事物无限分割的思想,用图形语言表示为图1,按此图分割的方法,可得到一个等式(符号语言):1=![]()
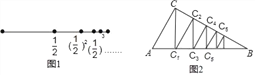
图2也是一种无限分割:在△ABC中,∠C=90°,∠B=30°,过点C作CC1⊥AB于点C1,再过点C1作C1C2⊥BC于点C2,又过点C2作C2C3⊥AB于点C3,如此无限继续下去,则可将利△ABC分割成△ACC1、△CC1C2、△C1C2C3、△C2C3C4、…、△Cn﹣2Cn﹣1Cn、….假设AC=2,这些三角形的面积和可以得到一个等式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星光厨具店购进电饭煲和电压锅两种电器进行销售其进价与售价如表
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,厨具店购进这两种电器共30台,用去了5600元,并且全部售完,问厨具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度厨具店决定采购电饭煲和电压锅共50台,且电饭煲的数量不大于电压锅的![]() ,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
,请你通过计算判断,如何进货厨具店赚钱最多?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,如果对角线AC和BD相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)在“平行四边形、矩形、菱形,正方形”中, 一定是等角线四边形(填写图形名称);
(2)若M、N、P、Q分别是等角线四边形ABCD四边AB、BC、CD、DA的中点,当对角线AC、BD还要满足 时,四边形MNPQ是正方形;
(3)如图2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D为平面内一点.若四边形ABCD是等角线四边形,且AD=BD,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com